Increased difficulty level. Lever arm. Equilibrium of forces on a lever Dynamics of motion of a material point in a circle. Centripetal and tangential forces. Leverage and moment of force. Moment of inertia. Equations of rotational motion of a point

The part of dynamics that studies the conditions of equilibrium of bodies is called static(gr. statos - standing).

The equilibrium of a body is a position that is maintained without additional influences. Based on the equations of dynamics of translational and rotational motions, we can formulate the following conditions for the equilibrium of a rigid body.

A body will not go into rotational motion if for any axis the sum of the moments of forces acting on it is equal to zero:

A body will not begin to move translationally if the sum of the forces acting on it is zero:

Equality (7.8) is called the rule of moments.

The conditions for equilibrium of a body at rest are the simultaneous equality to zero sum of forces And sum of moments of forces, acting on the body.

Let us find out what position the axis of rotation must occupy so that the body fixed to it remains in equilibrium under the action

In accordance with rule of moments For equilibrium it is necessary that the sum of the moments of all these forces relative to the axis equals zero.

It can be shown that for each body there is a single point where the sum of the moments of gravity about any axis passing through this point is equal to zero. This point is called center of gravity (usually coincides with the center of mass).

Body center of gravity (CG) is the point relative to which the sum of the moments of gravity acting on all particles of the body is equal to zero.

Thus, the force of gravity does not cause the body to rotate around the center of gravity. Therefore, all gravity forces could be replaced by a single force, which attached to this point and is equal to the force of gravity.

A common center of gravity (GCG) is often introduced for an athlete's body.

Basic properties of the center of gravity:

if the body is fixed on an axis passing through the center of gravity, then the force of gravity will not cause it to rotate;

the center of gravity is the point of application of gravity;

in a uniform field of gravity, the center of gravity coincides with the center of mass.

Equilibrium is a body position in which it can remain at rest for as long as desired. At

stable equilibrium (Fig. 7.11, a) - with a small deviation of the body from the equilibrium position, a force arises that tends to return the body to its original state;

indifferent equilibrium (Fig. 7.11, b) - with a small deviation the body remains in the equilibrium position;

unstable equilibrium (Fig. 7.11, c) - with a small deviation of the body from the equilibrium position, forces arise that tend to increase this deviation.

Example indifferent equilibrium is the equilibrium of a body fixed on an axis passing through its center of gravity. If the axis passes through another point and the center of gravity is located higher axis, then it is only possible unstable equilibrium. There will be balance sustainable, if the center of gravity is located below axes.

In a stable equilibrium position, a body has minimal potential energy.

Let us now consider the equilibrium of a body resting not on one point, as in the example with a ball, but on a whole area. In these cases, the condition for stability is as follows: for balance, it is necessary that the vertical drawn through the center of gravity pass inside the area of ​​the body’s support.

Violation of this condition leads to the impossibility of maintaining balance. For example, the cylinder shown in Fig. 7.12, a, must capsize, because the plumb line drawn through the CG passes outside its base.

A standing person maintains balance as long as the plumb line from the GCT is inside the area limited by the edges of his feet, Fig. 7.12, b.

A person sitting on a chair holds his torso upright, fig. 7.12, c. The GCT of the torso is located inside the body (near the spine, approximately 20 cm above the level of the navel). A plumb line drawn down from the GCP passes through the area of ​​support limited by the feet and legs of the chair. You can sit in this position. However, in order to stand up, a person must move the line of gravity inside the area limited by the feet. To do this, you need to tilt your torso forward and at the same time move your legs back (you can stand up without changing the position of your legs if you tilt forward sharply).

The simplest mechanisms

The action of the simplest mechanisms used to change the magnitude or direction of force is based on the use of the laws of statics.

Lever arm - a solid body, often in the form of a rod, which can rotate (rotate) around a fixed axis.

Let the axis divide the lever in the ratio L,:L, and two parallel forces F act on it, and F 2 (Fig. 7.13). We will also assume that the force of gravity acting on the lever can be neglected.

Let us determine the position of the rotation axis (O) at which the lever will remain in balance.

Equilibrium of the lever occurs under the condition that the ratio of the parallel forces applied to its ends is inverse to the ratio of the arms

and the moments of these forces are opposite in sign. Therefore, by applying a small force to the long end of the lever, it is possible to balance the much larger force applied to the short end of the lever. Depending on the relative position of the points of application of forces and the axis, levers of the 1st and 2nd kind are distinguished (Fig. 7.13):

A) Lever of the 1st kind. The forces are located on both sides of the axis. Similar levers are a long pole, with the help of which a heavy stone is lifted (Fig. 7.14.).

b) Lever of the 2nd kind. The forces are located on one side of the support. This type includes, for example, a wheelbarrow (Fig. 7.15), when using it, the force of the hands is applied at the “maximum” distance from the wheel axis (maximum shoulder), which makes it possible to transport large loads.

The use of leverage in mechanisms gives a gain in strength, while the same amount is lost in movement. The lever does not give any gain in work.

Many joints operate on the principle of a second-class lever. At the same time, the muscles act on a smaller shoulder lever, fig. 7.16. It leads to loss in power and to gain in movement And speed. As a result, with a relatively small movement, a muscle, link or limb describes a significantly larger trajectory.

This feature in the structure of the musculoskeletal nodes should cause additional complications in central regulation

Balance(French balancier - rocker) - a double-arm lever that performs rocking (oscillating) movements around a fixed axis. It is used in a balancing pendulum used in mechanotherapy.

Block, like the lever, it belongs to the simplest mechanisms, Fig. 7.17. It is made in the form of a disk that rotates freely on an axis. Along the circumference of the disk there is a groove for a chain (rope, thread). Equal tension is used at all points of the chain, which moves without friction.

Fixed block(Fig. 7.17, a) does not give a gain in strength, but allows you to change it direction. Yes, you can lift the load up, acting on the rope with a downward force, which is less tiring: F- R.

Movable block(Fig. 7.17, b) gives two-

For ease of use, a movable block is often used in combination with a fixed one (Fig. 7.17, c).

Block-type devices are used in mechanotherapy for training to facilitate (restore) movements in joints and strengthen muscles.

The simplest mechanisms include inclined plane. When describing the position of the body in this case, a rectangular coordinate system is used, the OX axis of which is directed parallel to the plane, and the OU axis is directed perpendicular to it. On a body located on an inclined plane, Fig. 7.18, gravity acts mg, ground reaction force - N and friction force F The projections of gravity onto the coordinate axes are equal to mg-sina (rolling force) and mgcosa.

When moving down an inclined plane, the rolling force assists the movement and contributes to a significant increase in speed. For a given length of an inclined plane, the rolling force is directly proportional to the height, Fig. 7.19.

An inclined surface is often used in training when performing various exercises, Fig. 7.20.

Changing the angle of inclination and the location of fastening of the fixing belts (at the level of large joints of the legs, lumbar and thoracic spine) allows you to dose the load on the musculoskeletal, cardiovascular and vestibular systems.

Elements of mechanics of the human musculoskeletal system

The human musculoskeletal system consists of interconnected skeletal bones. The bones of the skeleton act as levers that have a fulcrum in the joints or in the external environment and are driven by the traction force generated by the contraction of the muscles attached to the bones.

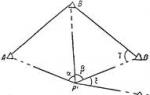
Lever of the first kind, providing movement or balance of the head in the sagittal plane.

In Fig. Figure 7.22 shows a skull and the forces acting on it.

The axis of rotation (O) passes through the articulation of the skull with the first vertebra. The skull is acted upon by two forces applied on opposite sides of the axis.

The force of gravity (/?) applied to the center of gravity of the skull. The leverage of this force is indicated by the letter

b. (F), Traction strength of muscles and ligaments attached to the occipital bone. The leverage of this force is indicated by the letter

A. F- Lever equilibrium condition: = a. Rb In this case a > b, F < hence,. R

Therefore, the lever gives a gain in strength, but a loss in movement.

The human forearm works on the principle of a second-class lever.

In Fig. Figure 7.24 shows the forearm and hand with a load, as well as the forces acting on them.

The axis of rotation (O) is located in the elbow joint. The lever is acted upon by two forces applied on one side of the axis. The leverage of this force is indicated by the letter

The force of gravity (/?), equal to the weight of the load. The leverage of this force is indicated by the letter (F), Muscle traction force attached to the occipital bone. The leverage of this force is indicated by the letter

A. F- Lever equilibrium condition: = a. Rb transmitted by the biceps. The leverage of this force is indicated by the letter< Ь, a > b, F > hence,. A

the magnitude of muscle contraction. At the same time, there is a gain in the speed of movement: the hand moves 8 times faster than the muscle contracts.

Thus, the method of muscle attachment that exists in the human (animal) body provides the limbs with speed of movement, which is more important in the struggle for existence than strength. Man would be an extremely slow creature if his hands were not constructed according to this principle.

Bone traction systems for fractures

When healing broken bones, it is necessary to fix the damaged areas and remove the forces that normally act at the fracture site until it heals. To do this, various combinations of weights and blocks are used.

In Fig. 7.25, and shows an exhaust system using two identical weights and two blocks. In this case, the tension forces are 7", and G 2 are equal. The same conditions can be created in another way (Fig. 7.25, b), using one load and a combination of movable and fixed blocks. In this case, the total force acting on the leg is equal to the vector sum of two tension forces (Fig. 7.25, c). F, 9 = 20° to horizontal.

In Fig. 7.26a shows the Russell traction system used to fix a fractured femur. This system was obtained by adding to the system shown in Fig. 7.25, two more blocks to ensure connection with the knee. The hip is set at an angle

Solution
Let us apply the rule of moments for the lever relative to the support:

where L is the length of one fragment, N is the reaction force of the lever with which it acts on the upper load.

Upper load equilibrium condition:

. (2)

Solving system (1) – (2) with respect to T, we obtain:

,

which shows that equilibrium is possible when
.

2. The equilibrium condition of the upper load is written ……………………….. 3

3. An expression has been found for T…………………………………………….. 2

4. It was investigated at what masses m equilibrium is possible………….. 2

Z Challenge 2. Catapult
A catapult is installed on the floor, which shoots balls with a certain initial speed v 0 at a certain angle α to the horizon. After the shot, the ball jumps, elastically hitting the floor. The flight time between adjacent impacts is equal to T. The ball hit the wall (see figure) after time (3/4)T after the previous impact on the floor. At what height will the ball hit the wall? The acceleration due to gravity is g.
Solution
At maximum ball lift height

. (1)

The required height can be found from the equation

. (2)

Substituting (1) into (2), we find:

. (3)
Evaluation criteria
1. Recording the relationship (1) …………………………………………. 4

2. Recording the relationship (2) ………………………………………….. 4

3. Receiving an answer (3) ……………………………………………... 2
Problem 3. Expansion of an ideal gas
P When an ideal gas was transferred from state A to state B, its pressure increased in direct proportion to its volume (see figure), and the temperature increased from 60 0 C to 100 0 C. By what percentage did the volume of the gas increase?

Solution

Let's write the Clapeyron-Mendeleev equation:

.

According to the conditions of the problem
, where α is a constant coefficient. Then

. (1)

. (2)

From here. Then the desired increase in gas volume

.
Evaluation criteria
The Clapeyron-Medeleev equation is written ………………………. 2

Relationships (1) and (2) are written…………………………………….. 3

Temperatures converted to Kelvins……………………………3

Found δ V ……………………………………………………………. 2

Task 4. Unsuccessful modernization
An electric heating device with unknown resistance is powered by a battery with an emf equal to ε and consumes current I 0 .

Wanting to increase the heating effect of the device, the operator took another source with the same EMF (but unknown internal resistance) and connected it first in series and then in parallel with the first source. However, in neither case did the amount of heat generated by the device change. What is the source resistance?

Since in each of the circuits the amount of heat released per unit time at the resistance R does not change, the current strength through it also does not change (i.e. it is equal to I 0. Joule-Lenz law).

Let's write Ohm's law for each of the electrical circuits (see Figures 1, 2, 3):

, (1)

, (2)

as well as the law of conservation of charge in node A of the circuit (Fig. 3)

I 0 = I 1 + I 2. (4)

Solving the system of equations (1 – 4), we find:

, with I 1 = I 0, I 2 = 0.

Evaluation criteria
1. Statement that the current through resistance R is the same....2

2. Recording of Ohm’s law for each of the circuits……………………………. 4

3. Recording the law of conservation of charge in node A of the circuit……………………… 1

4. Finding source resistances…………………………….. 3

Problem 5. Untwisted shaft.
A thread is wound on a homogeneous shaft, capable of rotating around a fixed horizontal axis, to the end of which a constant force F is applied (see figure). When the point of application of this force M has passed the path S = 40 cm, the shaft rotation speed has reached n 1 = 50 rpm. What will be the speed of the shaft when point M passes another 80 cm? The rotation of the shaft began from a state of rest. Ignore friction.
R decision
When point M passes the same distance as from the moment it began to move, the work done by force F will become twice as large. Consequently, according to the law of conservation, the kinetic energy of the shaft will become three times greater. But it is proportional to the square of its angular velocity (since the speed of each particle of the shaft is proportional to its angular velocity), therefore the desired shaft rotation speed can be found from the relation

. (1)

From here:
.

2. Statement that the kinetic energy of the shaft is proportional

square of the angular velocity of the shaft……………………………………2

2.Relation (1) was written and the answer was received………………………. 4

Example 1. Determine the support reactions of the beam (Fig. 1, Lever equilibrium condition: ), the ends of which are hinged. The beam is loaded by a couple of forces with a moment of kNm.

Fig.1

Solution. First of all, it is necessary to outline the direction of the support reactions (Fig. 1, b). Since a pair of forces is applied to the beam, it can only be balanced by a pair of forces. Consequently, the reactions of the supports are equal in magnitude, parallel, but opposite in direction. Let's replace the action of the supports with their reactions. Right support A- plane, therefore, the direction of the support reactionR Aperpendicular to this plane, and the support reactionR Bparallel to it and in the opposite direction. The beam is in equilibrium, so the sum of the moments of the pairs of forces applied to it is equal to zero:

where

KN.

Answer: kN.

Example 2. timber AB with a left articulated movable support and a right hinged fixed one, loaded with three pairs (Fig. 1), the moments of which kNm, kNm, kNm . Determine the reactions of the supports.

Fig.1

Solution. 1. Pairs of forces act on the beam, therefore, they can only be balanced by a pair, i.e. at points A And IN from the side of the supports, reactions of the supports must act on the beam, forming a pair of forces. At the point A the beam has a hinged and movable support, which means that the reaction is directed perpendicular to the supporting surface, i.e., in this case, perpendicular to the beam. Let's denote this reactionR Aand point it up. Then at the point IN from the side of the hinged-fixed support, a vertical force also actsR B, but down.

2. Based on the chosen direction of the pair forces (R A, R B) its moment (or ).

3. Let's create an equilibrium equation for pairs of forces:

Substituting the moment values ​​into this equation, we get

From here R A= 5 kN. Since the strengthR A And R Bform a pair, thenR B =R A= 5 kN.

Answer: kN.

Example3 . Load weighingG= 500 N suspended from a rope wound on a drum of radiusr= 10 cm. The drum is held by a pair of forces applied to the ends of a handle lengthl = 1.25 m, fastened to the drum and lying in the same plane with the rope. Determine Axle Reaction ABOUTdrum and couple power, FF", if they are perpendicular to the handle (Fig. 1,

Fig.1

Solutiona). . Let's consider the balance of forces applied to the drum: vertical weight force G F, a pair made up of forces And F", and reactions R o = 1.25 m, fastened to the drum and lying in the same plane with the rope. Determine Axle Reaction cylindrical hinge . Let's consider the balance of forces applied to the drum: vertical weight force, a pair made up of forces hence, , the magnitude and line of action of which are unknown. Since a pair of forces can only be balanced by a pair of forces lying in the same plane, then the forces Odrum and couple power, And must constitute a pair of forces, balanced by a pair . Let's consider the balance of forces applied to the drum: vertical weight force. Line of action of forceknown, reactionR o = 1.25 m, fastened to the drum and lying in the same plane with the rope. Determine Axle Reaction hinge . Let's consider the balance of forces applied to the drum: vertical weight force direct parallel to the force

in the opposite direction (Fig. 1, b). The force modules must be equal, i.e.Load weighing R o =

= 500 H.

The algebraic sum of the moments of two pairs of forces applied to the drum must be equal to zero: = 10 cm. The drum is held by a pair of forces applied to the ends of a handle length- Where drum and couple power, And;

= 500 N suspended from a rope wound on a drum of radius - couple's shoulder . Let's consider the balance of forces applied to the drum: vertical weight force, couple's shoulder .

R o F:

Finding force modules

Answer: N.

N; N.. Example 4 AB= 10 m has a hinged-fixed support A and articulated movable support IN with an inclined reference plane making an angle = 30° with the horizon. The beam is acted upon by three pairs of forces lying in the same plane, the absolute values ​​of the moments of which are:

kNm ;

kNm ;, if they are perpendicular to the handle (Fig. 1,

Fig.1

SolutionkNm. AB Determine the reactions of the supports (Fig. 1,R B. Let us consider the equilibrium of forces applied to the beamR A: three pairs of forces, ground reaction hence, , directed perpendicular to the reference plane, and the reaction of the support, a pair made up of forces hence, , the line of action of which is unknown (Fig. 1, b). Since the load consists only of pairs of forces lying in the same plane, then the reactions of the supportsA

BR Amust form a pair of forces lying in the same plane and balancing the given pairs of forces.R BLet's direct the reaction hence, , directed perpendicular to the reference plane, and the reaction of the support, a pair made up of forces hence, , the line of action of which is unknown (Fig. 1, b). Since the load consists only of pairs of forces lying in the same plane, then the reactions of the supportsparallel to the reaction

so that strength

The algebraic sum of the moments of two pairs of forces applied to the drum must be equal to zero:

From here

formed a pair of forces directed in the direction opposite to the clockwise rotation (Fig. 1, b).

For four pairs of forces applied to the beam, we use the equilibrium condition for pairs of forces lying in the same plane:R A And R B kN. The plus sign in the answer indicates that the accepted direction of the support reactions

formed a pair of forces directed in the direction opposite to the clockwise rotation (Fig. 1, b).

Answer: kN.

matcheswith true:Example 5. Two disks with diameters Example 5 2 Ddrum and couple power 1 = 200 mm and drum and couple power 2 = 100 mm fixed to the shaft (Fig. 1). The shaft axis is perpendicular to their plane. The disks rotate at a constant angular velocity. Powersdrum and couple power 1 and drum and couple power located in the plane of the disks and directed tangentially to them. Define strength

Fig.1

Solution.2 if

.

1 = 500 N.

The shaft with disks, according to the conditions of the problem, rotates at a constant angular velocity, therefore, the torques must be balanced, i.e. Since the shaft axis is perpendicular to the plane of action of the forces, then

Finding force modules

(The minus sign indicates the direction of the moment counterclockwise when viewed along the axis from its positive direction).

Answer: from here

Example6 . When calculating the strength of shafts, it is necessary to determine the moments of internal forces in sections perpendicular to the shaft axis. The resulting moment of internal forces relative to the longitudinal axis of the shaft is usually called torque and is designated differently from the moments of external forces, which are usually called torques. N. To a rectangular parallelepiped, the length of whose edges isA=100 cm, b= 120 cm,drum and couple power 1 , F" 1 , F 2 , And With F 3 , And= 160 cm, three mutually balanced pairs of forces are applieddrum and couple power 1 = And 2 and

Fig.1

Solution3. The forces of the first pair have a modulus

1 = 4 N. Determine the modules of the remaining forces (Fig. 1). = 1.25 m, fastened to the drum and lying in the same plane with the rope. Determine Axle Reaction the moment of each pair of forces, directing it perpendicular to the plane of action of the pair so that, looking towards it, we see the corresponding pair of forces tending to rotate this plane in the direction opposite to the clockwise rotation:

Moment modules:

Ncm;

We construct a closed triangle of moments of pairs of forces.

From Example 5EOC

From the triangle of moments

Ncm;

Ncm.

Modules of the forces that make up the pairs:

N;

N.

Answer: N; N.

Example 7. The ends of the beam are hinged at points A And IN(Fig. 1, a). Pairs of forces are applied to the beam, the moments of which are equal to kNm; kNm. Beam axis AB coincides with the plane of action of the pair of forces. Distance between supports= 10 cm. The drum is held by a pair of forces applied to the ends of a handle length= 3 m. Determine the support reactions of the beam, not taking into account the gravity of the beam.

Fig.1

Solution. Since 2 pairs of forces are applied to the beam, they can only be balanced by a pair of forces. This means that the reactions of the supports are equal in magnitude, parallel, but opposite in direction. We replace the actions of the supports with their reactions (Fig. 1 , b). The beam is in equilibrium, so the sum of the moments of pairs of forces opposite to it is equal to zero:

formed a pair of forces directed in the direction opposite to the clockwise rotation (Fig. 1, b).

Answer: kN.

Example8 . The shaft, on which three gears are mounted, rotates around a fixed axis. Powersdrum and couple power 1 , drum and couple power 2 and drum and couple power 3 located in planes perpendicular to the axis of rotation and directed tangent to the circles of the gears, as shown schematically in Fig. 1. Powersdrum and couple power 2 = 400 H, drum and couple power 3 = 200 H . Gear diameters = 100 mm, = 200 mm,= 400 mm. Calculate the magnitude of the moments of forces F 1 , drum and couple power 2 and drum and couple power 3 relative to the axis of rotation and force modulus F 1 attached to a disk with a diameterExample 5 1 .

Fig.1

Solution. Since the shaft axis is perpendicular to the plane of action of the forces, then:

Nm;

Nm.

(The minus sign for a moment indicates the clockwise direction of the moment when viewed along the axis from its positive direction.)

The torques must be balanced:

Then

Nm;

Finding force modules

Answer: Nm, Nm, N × m, N.

Example 9.CargoLoad weighingcreates pressing force using a leverdrum and couple powerper detail A(Fig. 1, Lever equilibrium condition: ). Lever arms N.= 300 mm,A= 900 mm. Determine the force of gravity of the load if the clamping force is 400 N.

Fig.1

Solution. On the design diagram of the lever (Fig. 1, b) to the point A load weight appliedLoad weighing, to the point IN– joint reaction force, to the point WITH a reaction force is applied equal in modulus to the clamping forcedrum and couple power(Newton's 3rd law).

Let's create an equilibrium equation for the lever relative to the point IN :

in this case the moment of force relative to the point IN equals 0.

Answer: N.

Example 10. Determine clamping forcedrum and couple powerper detail A(Fig. 1, Lever equilibrium condition: ), created using a lever and a weightLoad weighing= 300 H . Lever RatioA / a = 3.

Fig.1

Solution.Let's consider the balance of the lever. To do this, we replace the action of the supports with their reactions (Fig. 1, b).

Clamping forcedrum and couple powerper detail A modulo equal to the reaction force (this follows from Newton’s 3rd law).

Let us write down the equilibrium condition of the lever relative to the point IN :

Answer: N.

Example 11.Three disks are rigidly fixed to the shaft (Fig. 1, a). Drive disk 1 transmits torque Nm. Moment applied to driven disk 2, Nm. Disc diametersExample 5 1 = 0.2 m, Example 5 2 = 0.4 m, Example 5 3 = 0.6 m. Determine the magnitude and direction of the moment on disk 3, provided that the shaft rotates uniformly. Calculate also the circumferential forcesdrum and couple power 1 , drum and couple power 2 and drum and couple power 3 , attached to the corresponding discs. These forces are directed tangentially to the circumference of the disk and are located in planes perpendicular to the shaft axis.

Fig.1

Solution. The shaft with disks, according to the conditions of the problem, rotates uniformly, therefore, the torques must be balanced (Fig. 1, b):

, Nm.

Let's determine the circumferential forcesdrum and couple power 1 , drum and couple power 2 , drum and couple power 3 :

, , N, kN;

, , N, kN;

, , N, N.

Answer: N × m, N, N, N.

Example 12. To a rod supported at points A And IN (Fig. 1, a), two pairs of forces are applied, the moments of which To Nm and to Nm. Distance N.= 0.4 m. Determine the reaction of the stops A And IN, without taking into account the gravity of the rod. The plane of action of the force pairs coincides with the axis of the rod.

Fig.1

Solution. Since only pairs of forces are applied to the rod, they can only be balanced by a pair of forces. This means that the reactions of the supports are equal in magnitude, but opposite in direction (Fig. 1, b).

The rod is in equilibrium, so

, ,

kN,

The minus sign indicates the direction of the moment of force pairs and .

Answer: kN, kN.

Example 13. On the lever at the point WITH force actsdrum and couple power= 250 H (Fig. 1, a ). Determine the force applied to the brake discs at the point A, if the length of the leverC.B.= 900 mm, distanceCD= 600 mm.

Fig.1

Solution.Let us replace the actions of the supports with lever by their reactions (Fig. 1, b). Lever equilibrium equation:

;

Finding force modules

The force applied to the brake discs at the point A, is equal in modulus (according to Newton’s third law).

Answer: from here

Example 14. The shoe brake holds the shaft at rest, to which a pair of forces with a torque of Nm is applied. Brake disc diameterExample 5= 400 mm (Fig. 1 , A). Determine with what force the pads must be pressed against the brake disc so that the shaft remains at rest. The coefficient of static friction between the brake disc and pads is assumed to bef = 0,15.

Fig.1

Solution. In order for the shaft to remain at rest, the moments must be equal M and (Fig. 1, b):

where is the moment created by a pair of friction forces.

Let us determine the friction force by knowing the friction coefficientfrest between the brake disc and pads:

Then

Finding force modules

Answer: kN.

Example 15. Two disks with diameters ofExample 5 1 = 220 mm and Example 5 2 = 340 mm (Fig. 1, a). To the first disc force applied drum and couple power 1 = 500 N. The line of action of the force is located in a plane perpendicular to the shaft axis. Determine the magnitude and direction of the force that must be applied to the second disk so that the shaft rotates evenly. Calculate the torques on each disk.

Fig.1

Solution. Disc torques:

(The minus sign for a moment indicates the direction of the moment counterclockwise when viewed along the axis from its positive direction.)

Since the shaft rotates uniformly, the torques must be balanced (Fig. 1, b):

N × m,N × m,

, , Finding force modules

The direction of force is opposite to the direction of force

Answer: N × m,N × m, N.

Example 16.A load kN, raised using a cable wound on a drum with a diameter of m, is held at rest by a ratchet mechanism consisting of a gear with a design diameter of m and a thrust lever (Fig. 1, a). Neglect the weight of the mechanism parts, as well as friction. Determine the force loading the thrust lever.

Fig.1

Solution.We will consider the equilibrium of the block. An external connection is applied to it - a persistent lever. Let's replace it with a reaction. In this problem there is one unknown, which, according to Newton’s third law, is equal to the reaction (Fig. 1, b).

,

where we have:

, kN.

formed a pair of forces directed in the direction opposite to the clockwise rotation (Fig. 1, b).

Answer: kN.

Example 17.The force applied by a person to the end of the handle of a manual lever press is equal todrum and couple power= 120 H. Having accepted AC= 220 mm and AB= 40 mm, determine the pressure force of the piston on the pressed material (Fig. 1, a). A And IN Fastening at points

Fig.1

Solutionarticulated. Neglect the weight of the mechanism parts, as well as friction.

. Finding force modules

Answer: from here

. The piston pressure force is equal to the reaction force acting from the piston on the handle (Fig. 1, b). Let's create an equation for the moments of force for the handle:Example 18. In the tape transport mechanism of the device, the tape is kept taut using a double-armed lever ABC(Fig. 1, a) AB. There is a pressure roller at one end of the lever, the other end is pulled back by a spring band with an elastic force of 4 N. Determine the force of pressure of the roller on the tape, assuming that the common normal at the point of contact is vertical. Accept = 50 mm and Sun

Fig.1

Solution= 10 mm. Neglect the weight of the mechanism parts, as well as friction. In the tape transport mechanism of the device, the tape is kept taut using a double-armed lever. On the lever

external connections are imposed. Let's get rid of them by replacing their action with reaction forces (Fig. 1, b). In this problem, one unknown is the pressure force of the roller on the tape, which is equal to the reaction force

Let's create an equation for the moments of forces:

Finding force modules

Answer: from here

Where do we get:Example 19.drum and couple powerA load weighing 950 N is lifted uniformly using a gate consisting of a drum with a diameter of 0.14 m and a handle with a shoulder of 0.4 m (Fig. 1).

Fig.1

Solution. In this problem, there is one unknown – force (Fig. 1, b). To find it, we write the equation of moments of forces:

, , .

Finding force modules

Answer: from here

Example 20.To transfer a homogeneous column AB from a horizontal to a vertical position, one end of it was hooked with a crane cable, and a stop was attached to the other end (Fig. 1, a).

Fig.1

SolutionDetermine the tension force of the cable at the moment the column begins to rise, if its weight is 3 kN and its length is 4 m.

;

KN.

Answer: kN.

. To find the tension force of the cable, we create an equation for the moments of force (Fig. 1, b):

A lever is a rigid body that can rotate around a fixed point.

A fixed point is called a fulcrum.

A familiar example of a lever is a swing (Fig. 25.1). When do two people on a seesaw balance each other?

Let's start with observations. You, of course, have noticed that two people on a swing balance each other if they have approximately the same weight and are at approximately the same distance from the fulcrum (Fig. 25.1, a).

Rice. 25.1. Balance condition for a swing: a - people of equal weight balance each other when they sit at equal distances from the fulcrum; b - people of different weights balance each other when the heavier one sits closer to the fulcrum

If these two are very different in weight, they balance each other only if the heavier one sits much closer to the fulcrum (Fig. 25.1, b).

Let us now move from observations to experiments: let us find experimentally the conditions for equilibrium of the lever.

Let's put experience

Experience shows that loads of equal weight balance the lever if they are suspended at equal distances from the fulcrum (Fig. 25.2, a).

If the loads have different weights, then the lever is in equilibrium when the heavier load is as many times closer to the fulcrum as its weight is greater than the weight of the light load (Fig. 25.2, b, c).

Rice. 25.2. Experiments to find the equilibrium condition of a lever Lever equilibrium condition.

The distance from the fulcrum to the straight line along which the force acts is called the arm of this force. Let us denote F 1 and F 2 the forces acting on the lever from the side of the loads (see diagrams on the right side of Fig. 25.2). Let us denote the shoulders of these forces as l 1 and l 2, respectively. Our experiments have shown that the lever is in equilibrium if the forces F 1 and F 2 applied to the lever tend to rotate it in opposite directions, and the modules of the forces are inversely proportional to the arms of these forces:

F 1 /F 2 = l 2 /l 1.

This condition of lever equilibrium was experimentally established by Archimedes in the 3rd century BC. e.

You can study the equilibrium condition of a lever experimentally in laboratory work No. 11.

1. The figure schematically shows a staircase AC, leaning against the wall.

What is the moment of reaction force of the support acting on the ladder relative to the point WITH?

2. Forces and are applied to a thin homogeneous rod at points 1 and 3. Through what point must the axis of rotation pass for the rod to be in equilibrium? Neglect the mass of the rod.

3. The balance beam, from which two bodies are suspended on threads (see figure), is in equilibrium.

How should the mass of the first body be changed so that, after increasing the shoulder by 3 times, the balance is maintained? (The rocker and threads are considered weightless.)

1) increase 3 times

2) increase 6 times

3) reduce by 3 times

4) reduce by 6 times

4. A body capable of rotating around an axis passing through point (.) O is acted upon by forces F₁, F₂, F₃, F₄.

This body is under the influence of forces

1. rotates clockwise

2. rotates counterclockwise

3. is at rest

5. Under the influence of gravity of the load and force F the lever shown in the figure is in equilibrium.

Force vector F perpendicular to the lever. The distances between the points of application of forces and the fulcrum, as well as the projections of these distances onto the vertical and horizontal axes are shown in the figure. If the force module F is equal to 120 N, then the modulus of gravity acting on the load is equal to

A basic level of

1.Task text:

Forces of 24 and 27 N were applied to the ends of the weightless lever. The length of the lever is 17 cm. Find the arms of the lever.

2. Task text:

What force must be applied to place a uniform rod 2 m long and weighing 100 kg lying on the ground vertically?

3. Task text:

A log 12 m long can be balanced horizontally on a stand 3 m from its thick end. If the stand is in the middle and a weight of 60 kg is placed on the thin end, then the log will again be in balance. Determine the mass of the log.

Solution:

4. Task text:

A rail 10 m long and weighing 900 kg is lifted on two parallel cables. Determine the tension force of the cables if one of them is attached to the end of the rail, and the second is at a distance of 1 m from the other end.

5. Task text:

What is the minimum horizontal force that must be applied to the upper edge of a cube of mass m, located on a horizontal plane in order to throw it over the lower edge?

Increased difficulty level

1. Task text:

The load is held in place by a lever, applying a vertical force of 400 N (see figure). The lever consists of a hinge and a homogeneous rod with a mass of 20 kg and a length of 4 m. The distance from the hinge axis to the point where the load is suspended is 1 m. What is the mass of the load? Give your answer in kilograms.

2. Task text:

Weights of masses 40 kg and 10 kg are suspended from the ends of a rod with a mass of 10 kg and a length of 40 cm. Where should the rod be supported so that it is in balance?

Solution:

3. Task text:

A homogeneous beam weighing 20 kg lies at its ends on supports, the distance between which is 6 m. At a distance of 1 m from the right support, a load weighing 300 kg is located on the beam. Determine the force with which the beam presses on each support.

4. Task text:

A beam of mass 800 kg is 4 m long and is supported at a distance of 1.9 m from its left end. At what distance from this end must a person weighing 80 kg stand on the beam for the beam to remain in balance?

5. Text of the problem:

A homogeneous beam with a mass of 80 kg and a length of 5 m is carried by two people. One person supports the beam at a distance of 1 m from its end, and the second holds the opposite end of the beam. Determine the magnitude of the force that the beam exerts on the second person.