سخنرانی در مورد ریاضیات با موضوع "تست عمود بودن دو صفحه". استریومتری ثابت کنید که دو صفحه عمود بر هم هستند

عمود بودن صفحات تعریف. اگر زاویه خطی در لبه زاویه دو وجهی بین این صفحات یک خط مستقیم باشد، دو صفحه عمود نامیده می شوند.
امضا کردنعمود بودن صفحاتاگر صفحه ای از خطی عمود بر صفحه دیگر عبور کند، این صفحات عمود هستند.
اثبات اجازه دهید آو - دو صفحه متقاطع، با- خط تقاطع آنها و آ- سر راست عمود بر صفحه? و دراز کشیدن در هواپیماآ. الف - نقطه تلاقی خطوطآو با.داخل یک هواپیما؟ از نقطهو بازیابی خواهیم کرد عمود باشد، و بگذارید یک خط مستقیم باشد. ب آسر راستعمود بر عمود باشد، و بگذارید یک خط مستقیم باشدسطح؟ یعنی عمود بر هر خط مستقیمی در این صفحه یعنی خطوط مستقیم است باو . عمود بر آزاویه بین خطوط مستقیم وب - آهواپیماهای خطی وو برابر 90 درجه است، بنابراین چگونه آسر راستعمود باشد، و بگذارید یک خط مستقیم باشدعمود بر یک خط مستقیمآ(اثبات).با تعریف هواپیما و

عمود بر.. قضیه 1اگر از نقطه ای متعلق به یکی از دو صفحه عمود بر هم رسم کنیم
عمود بر صفحه دیگر، پس این عمود به طور کامل در صفحه اول قرار دارد. آاثبات اجازه دهید و- صفحات عمود بر وبا - آخط مستقیم تقاطع آنها، A - نقطه با.صاف دراز کشیده آو مستقیماً متعلق به اجازه دهید عمود بر هواپیما؟ رسم شده از نقطه A در صفحه قرار ندارد، سپس نقطه C پایه است با.این عمود بر قرار دارد سطح؟ با.و به خط تعلق ندارداز نقطه A عمود AB را پایین می آوریمبه طور مستقیمخط AB عمود استهواپیما (من از قضیه 2 استفاده می کنم). ? از طریق خط مستقیم AB و نقطه Cیک هواپیما بکشیم؟ (یک خط مستقیم و یک نقطه یک صفحه را مشخص می کند و فقط یک صفحه). ما آن را در آ.

سطح. از یک نقطه A تا خط BC دو عمود رسم می شود که نمی تواند اتفاق بیفتد که به معنای خط AC استبا خط مستقیم AB منطبق است و خط مستقیم AB به نوبه خود کاملاً در صفحه قرار دارد
اثبات اجازه دهید آقضیه 2 واگر در یکی از دو صفحه عمود بر خط آنها عمود بکشیم تقاطع، آنگاه این عمود بر صفحه دوم عمود خواهد بود.و - دو صفحه عمود بر هم، باو دراز کشیدن در هواپیماآخط تقاطع آنها و آزاویه بین خطوط مستقیم با.آ -سر راست عمود بر یک خط مستقیم. الف - نقطه تلاقی خطوط آسطح؟ یعنی عمود بر هر خط مستقیمی در این صفحه یعنی خطوط مستقیم استعمود باشد، و بگذارید یک خط مستقیم باشدداخل هواپیما ? از نقطه A عمود را بازیابی می کنیم و اجازه می دهیم یک خط مستقیم باشدهواپیماها آو و برابر با 90 درجه است، زیرا هواپیماآو عمود بر. سر راست آعمود بر یک خط مستقیمعمود باشد، و بگذارید یک خط مستقیم باشد(طبق اثبات شده) و مستقیم بابا شرطپس مستقیم است آعمود بر هواپیما؟ (

این مقاله به صفحات عمود بر هم اختصاص دارد. تعاریف و نمادها همراه با مثال آورده خواهد شد. علامت عمود بودن صفحات و شرایطی که در آن برآورده می شود فرموله می شود. راه حل های مشکلات مشابه با استفاده از مثال ها مورد بحث قرار خواهند گرفت.

Yandex.RTB R-A-339285-1

اگر زاویه ای بین خطوط متقاطع وجود داشته باشد، می توانیم در مورد تعریف صفحات عمود بر هم صحبت کنیم.

تعریف 1

به شرطی که زاویه بین خطوط عمود بر هم 90 درجه باشد به آنها می گویند عمود بر.

تعیین عمودگرایی معمولاً با علامت "⊥" نوشته می شود. اگر شرط بیان کند که صفحات α و β عمود هستند، آنگاه ورودی به شکل α⊥ β است. تصویر زیر با جزئیات نشان می دهد.

وقتی در گیره داده می شود که صفحه α و β عمود هستند، این بدان معنی است که α بر β عمود است و بالعکس. چنین صفحاتی را متقابل عمود بر هم می گویند. به عنوان مثال، دیوار و سقف در یک اتاق متقابل عمود هستند، زیرا هنگامی که آنها را قطع می کنند، یک زاویه قائمه تشکیل می دهند.

عمود بودن صفحات - علامت و شرط عمود بودن

در عمل، می توانید با وظایفی روبرو شوید که در آن لازم است عمود بودن صفحات داده شده را تعیین کنید. ابتدا باید زاویه بین آنها را تعیین کنید. اگر برابر با 90 درجه باشد، از تعریف عمود بر هم در نظر گرفته می شوند.

برای اثبات عمود بودن دو صفحه، از علامت عمود بودن دو صفحه استفاده می شود. اجازه دهید تعریف دقیق معیار عمودگرایی را در قالب یک قضیه بنویسیم.

قضیه 1

اگر یکی از دو صفحه داده شده یک خط عمود بر صفحه دیگر را قطع کند، آنگاه صفحات داده شده عمود هستند.

اثبات در کتاب هندسه برای پایه های 10-11 موجود است که در آن توضیحات مفصلی وجود دارد. از علامت چنین بر می آید که اگر صفحه ای بر خط تقاطع دو صفحه معین عمود باشد، بر هر یک از این صفحات عمود است.

برای اثبات شرط لازم و کافی وجود دارد. بیایید آنها را برای عمود بودن دو صفحه داده شده در نظر بگیریم، که به عنوان بررسی عمود بودن آنها، واقع در یک سیستم مختصات مستطیلی از فضای سه بعدی استفاده می شود. برای اینکه اثبات معتبر باشد، لازم است تعریف بردار نرمال یک صفحه را اعمال کنیم که به اثبات شرط لازم و کافی برای عمود بودن صفحات کمک می کند.

قضیه 2

برای آشکار بودن عمود بودن صفحات متقاطع، کافی و لازم است که بردارهای نرمال صفحات داده شده در زوایای قائمه همدیگر را قطع کنند.

اثبات

بگذارید یک سیستم مختصات مستطیلی در فضای سه بعدی مشخص شود. اگر n 1 → = (A 1, B 1, C 1) و n 2 → = (A 2, B 2, C 2) داشته باشیم که بردارهای عادی صفحات داده شده α و β هستند، آنگاه لازم و کافی شرط عمود بردارهای n 1 → و n 2 → شکل خواهد گرفت

n 1 → ، n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B 2 + C 1 · C 2 = 0

از اینجا دریافت می کنیم که n 1 → = (A 1, B 1, C 1) و n 2 → = (A 2, B 2, C 2) بردارهای نرمال صفحات داده شده هستند و برای واقعیت عمود بودن α و β لازم و کافی است، به طوری که حاصل ضرب اسکالر بردارهای n 1 → و n 2 → برابر با صفر است و بنابراین به شکل n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 به خود می گیرد. · B 2 + C 1 · C 2 = 0 .

برابری برآورده شده است.

بیایید نگاهی دقیق تر به مثال ها بیندازیم.

مثال 1

عمود بر صفحات مشخص شده در سیستم مختصات مستطیلی O x y z فضای سه بعدی مشخص شده توسط معادلات x - 3 y - 4 = 0 و x 2 3 + y - 2 + z 4 5 = 1 را تعیین کنید؟

راه حل

برای یافتن پاسخ سوال عمودگرایی، ابتدا باید مختصات بردارهای عادی صفحات داده شده را پیدا کنید، پس از آن می توانید عمود بودن را بررسی کنید.

x - 3 y - 4 = 0 یک معادله کلی از صفحه است که از آن می توانید بلافاصله مختصات بردار نرمال را برابر با n 1 → = (1, - 3, 0) تبدیل کنید.

برای تعیین مختصات بردار نرمال صفحه x 2 3 + y - 2 + z 4 5 = 1، از معادله صفحه در بخش ها به یک معادله کلی حرکت می کنیم.

سپس دریافت می کنیم:

x 2 3 + y - 2 + z 4 5 ⇔ 3 2 x - 1 2 y + 5 4 z - 1 = 0

سپس n 2 → = 3 2, - 1 2, 5 4 مختصات بردار نرمال صفحه x 2 3 + y - 2 + z 4 5 = 1 هستند.

بیایید به محاسبه حاصل ضرب اسکالر بردارهای n 1 → = (1, - 3, 0) و n 2 → = 3 2, - 1 2, 5 4 برویم.

به دست می آوریم که n 1 → , n 2 → = 1 · 3 2 + (- 3) · - 1 2 + 0 · 5 4 = 3 .

می بینیم که برابر با صفر نیست، یعنی بردارهای داده شده عمود نیستند. نتیجه این است که هواپیماها نیز عمود نیستند. شرط برقرار نیست.

پاسخ:هواپیماها عمود نیستند

مثال 2

سیستم مختصات مستطیلی O x y z دارای چهار نقطه با مختصات A - 15 4, - 7 8, 1, B 17 8, 5 16, 0, C 0, 0, 3 7, D - 1, 0, 0 است. بررسی کنید که آیا صفحات A B C و A B D عمود هستند یا خیر.

راه حل

ابتدا باید حاصل ضرب اسکالر بردارهای این صفحات را محاسبه کنید. اگر برابر با صفر باشد فقط در این حالت می توان عمود بودن آنها را در نظر گرفت. مختصات بردارهای معمولی n 1 → و n 2 → صفحات A B C و A B D را پیدا می کنیم.

از مختصات داده شده نقاط، مختصات بردارهای A B → , A C → , A D → را محاسبه می کنیم. دریافتیم که:

A B → = 47 8، 19 16، - 1، A C → = 15 4، 7 8، - 4 7، A D → = 11 4، 7 8، - 1.

بردار نرمال صفحه A B C حاصلضرب برداری بردارهای A B → و A C → و برای A B D حاصلضرب برداری A B → و A D → است. از اینجا به آن می رسیم

n 1 → = A B → × A C → = i → j → k → 47 8 19 16 - 1 15 4 7 8 - 4 7 = 11 56 i → - 11 28 j → + 11 16 k → ⇔ n 1 → 56 , - 11 28 , 11 16 n 2 → = A B → × A D → = i → j → k → 47 8 19 16 - 1 11 4 7 8 - 1 = - 5 16 i → + 25 8 j → + 1 k → ⇔ n 2 → = - 5 16، 25 8، 15 8

بیایید شروع به یافتن حاصل ضرب اسکالر n 1 → = 11 56، - 11 28، 11 16 و n 2 → - 5 16، 25 8، 15 8 کنیم.

دریافت می کنیم: n 1 → ، n 2 → = 11 56 · - 5 16 + - 11 28 · 25 8 + 11 16 · 15 8 = 0.

اگر برابر با صفر باشد، بردارهای صفحات A B C و A B D عمود هستند، پس خود صفحات عمود هستند.

پاسخ:صفحات عمود بر هم هستند

می‌توان به روش متفاوتی به جواب نزدیک شد و از معادلات صفحات A B C و A B D استفاده کرد. پس از یافتن مختصات بردارهای نرمال این صفحات، می توان بررسی کرد که آیا شرط عمود بردارهای نرمال صفحات برقرار است یا خیر.

در صورت مشاهده خطایی در متن، لطفاً آن را برجسته کرده و Ctrl+Enter را فشار دهید

این درس به کسانی که مایل به درک موضوع "علامت عمود بر دو صفحه" هستند کمک می کند. در ابتدای آن تعریف زوایای دو وجهی و خطی را تکرار می کنیم. سپس در نظر خواهیم گرفت که چه صفحاتی عمود نامیده می شوند و علامت عمود بودن دو صفحه را ثابت می کنیم.

موضوع: عمود بودن خطوط و صفحات

درس: علامت عمود بودن دو صفحه

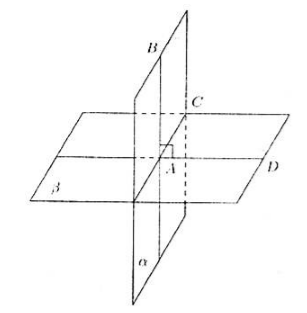
تعریف. زاویه دو وجهی شکلی است که از دو نیم صفحه تشکیل شده است که به یک صفحه تعلق ندارند و خط مستقیم مشترک آنها a (a یک لبه است).

برنج. 1

بیایید دو نیم صفحه α و β را در نظر بگیریم (شکل 1). مرز مشترک آنها l است. به این شکل زاویه دو وجهی می گویند. دو صفحه متقاطع چهار زاویه دو وجهی با یک لبه مشترک را تشکیل می دهند.

زاویه دو وجهی با زاویه خطی آن اندازه گیری می شود. یک نقطه دلخواه در لبه مشترک l زاویه دو وجهی انتخاب می کنیم. در نیم صفحه α و β از این نقطه عمودهای a و b را به خط مستقیم l رسم می کنیم و زاویه خطی زاویه دو وجهی را به دست می آوریم.

خطوط مستقیم a و b چهار زاویه برابر با φ، 180 درجه - φ، φ، 180 درجه - φ را تشکیل می دهند. به یاد بیاورید که زاویه بین خطوط مستقیم کوچکترین زاویه از این زاویه است.

تعریف. زاویه بین صفحات کوچکترین زاویه دو وجهی تشکیل شده توسط این صفحات است. φ زاویه بین صفحات α و β است، اگر

تعریف. دو صفحه متقاطع در صورتی که زاویه بین آنها 90 درجه باشد عمود بر یکدیگر (متقابل عمود) نامیده می شوند.

برنج. 2

یک نقطه دلخواه M در لبه l انتخاب شده است (شکل 2). اجازه دهید دو خط مستقیم عمود MA = a و MB = b را به ترتیب به لبه l در صفحه α و در صفحه β رسم کنیم. ما زاویه AMB را دریافت کردیم. زاویه AMB زاویه خطی یک زاویه دو وجهی است. اگر زاویه AMB 90 درجه باشد، صفحات α و β را عمود بر هم می گویند.

خط b از نظر ساخت بر خط l عمود است. خط b عمود بر خط a است، زیرا زاویه بین صفحات α و β 90 درجه است. متوجه شدیم که خط b بر دو خط متقاطع a و l از صفحه α عمود است. این بدان معنی است که خط مستقیم b عمود بر صفحه α است.

به طور مشابه، می توانیم ثابت کنیم که خط مستقیم a بر صفحه β عمود است. خط a بر اساس ساخت بر خط l عمود است. خط a عمود بر خط b است، زیرا زاویه بین صفحات α و β 90 درجه است. متوجه شدیم که خط a بر دو خط متقاطع b و l از صفحه β عمود است. این بدان معنی است که خط مستقیم a عمود بر صفحه β است.

اگر یکی از دو صفحه از خطی عمود بر صفحه دیگر عبور کند، چنین صفحاتی عمود هستند.

ثابت كردن:

برنج. 3

اثبات:

اجازه دهید صفحات α و β در امتداد خط مستقیم AC قطع شوند (شکل 3). برای اثبات عمود بودن صفحات باید یک زاویه خطی بین آنها ایجاد کنید و نشان دهید که این زاویه 90 درجه است.

خط مستقیم AB عمود بر صفحه β است و بنابراین بر خط مستقیم AC که در صفحه β قرار دارد.

اجازه دهید یک خط مستقیم AD عمود بر یک خط مستقیم AC در صفحه β رسم کنیم. سپس BAD زاویه خطی زاویه دو وجهی است.

خط مستقیم AB عمود بر صفحه β است و بنابراین بر خط مستقیم AD که در صفحه β قرار دارد. این به این معنی است که زاویه خطی BAD 90 درجه است. این بدان معنی است که صفحات α و β عمود هستند، که باید ثابت شود.

صفحه عمود بر خطی که دو صفحه داده شده در امتداد آن قطع می شوند، بر هر یک از این صفحات عمود است (شکل 4).

ثابت كردن:

برنج. 4

اثبات:

خط مستقیم l بر صفحه γ عمود است و صفحه α از خط مستقیم l می گذرد. این بدان معنی است که با توجه به عمود بودن صفحات، صفحات α و γ عمود هستند.

خط مستقیم l عمود بر صفحه γ است و صفحه β از خط مستقیم l می گذرد. این بدان معنی است که با توجه به عمود بودن صفحات، صفحات β و γ عمود هستند.

رابطه عمود بر صفحات در نظر گرفته می شود - یکی از مهم ترین و پرکاربردترین ها در هندسه فضا و کاربردهای آن.

از همه انواع ترتیبات متقابل

دو صفحه، صفحه ای که در آن صفحات عمود بر یکدیگر هستند، مستحق توجه و مطالعه ویژه هستند (مثلاً صفحات دیوارهای مجاور یک اتاق،

حصار و قطعه زمین، در و کف و غیره (شکل 417، a–c).

مثال‌های بالا به ما امکان می‌دهند یکی از ویژگی‌های اصلی رابطه را که مطالعه خواهیم کرد - تقارن مکان هر صفحه نسبت به دیگری را ببینیم. تقارن با این واقعیت تضمین می شود که به نظر می رسد صفحات از عمود بر هم بافته شده اند. بیایید سعی کنیم این مشاهدات را روشن کنیم.

اجازه دهید یک صفحه α و یک خط مستقیم c روی آن داشته باشیم (شکل 418، a). اجازه دهید از هر نقطه از خط c خطوط مستقیم عمود بر صفحه α رسم کنیم. همه این خطوط با یکدیگر موازی هستند (چرا؟) و بر اساس مسئله 1 § 8، صفحه خاصی β را تشکیل می دهند (شکل 418، b). طبیعی است که هواپیما را β بخوانیم عمود برهواپیما α.

به نوبه خود، تمام خطوطی که در صفحه α و عمود بر خطوط قرار دارند، صفحه α را تشکیل می دهند و بر صفحه β عمود هستند (شکل 418، ج). در واقع، اگر a یک خط دلخواه باشد، آنگاه خط c را در نقطه ای از M قطع می کند. یک خط مستقیم b عمود بر α از نقطه M در صفحه β می گذرد، بنابراین b a . بنابراین، a c، a b، بنابراین a β. بنابراین، صفحه α عمود بر صفحه β است، و خط مستقیم، خط تقاطع آنها است.

دو صفحه را عمود می گویند که هر یک از آنها با خطوط مستقیم عمود بر صفحه دوم و عبور از نقاط تلاقی این صفحات تشکیل شده باشد.

عمود بودن صفحات α و β با علامت آشنا نشان داده می شود: α β.

اگر قطعه ای از یک اتاق را در یک خانه روستایی در نظر بگیریم، می توان یک تصویر از این تعریف را تصور کرد (شکل 419). در آن کف و دیوار به ترتیب از تخته هایی عمود بر دیوار و کف ساخته شده است. بنابراین آنها عمود هستند. در تمرین

این بدان معنی است که کف افقی و دیوار عمودی است.

استفاده از تعریف فوق هنگام بررسی واقعی عمود بودن صفحات دشوار است. اما اگر استدلالی را که منجر به این تعریف شد به دقت تجزیه و تحلیل کنیم، می بینیم که عمود بودن صفحات α و β با وجود یک خط مستقیم b عمود بر صفحه α در صفحه β تضمین شده است (شکل 418، ج). . به معیار عمود بودن دو صفحه رسیدیم که بیشتر در عمل استفاده می شود.

406 عمود بر خطوط و صفحات

قضیه 1 (آزمون عمود بودن صفحات).

اگر یکی از دو صفحه از خطی عمود بر صفحه دوم عبور کند، این صفحات عمود هستند.

 اجازه دهید صفحه β از یک خط b عمود بر صفحه α عبور کند و خط تقاطع صفحات α و β است (شکل 420، a). تمام خطوط مستقیم صفحه β، موازی با خط b و قطع کننده خط c، همراه با خط مستقیم b صفحه β را تشکیل می دهند. با قضیه دو خط موازی که یکی از آنها عمود بر صفحه است (قضیه 1 § 19)، همه آنها همراه با خط b بر صفحه α عمود هستند. یعنی صفحه β شامل خطوط مستقیمی است که از خط تقاطع صفحات α و β و عمود بر صفحه α عبور می کنند (شکل 420، ب).

حال در صفحه α از نقطه A از محل تلاقی خطوط b و خطی عمود بر خط c رسم می کنیم (شکل 420، ج). خط مستقیم عمود بر صفحه β است، بر اساس عمود بودن خط مستقیم و صفحه (a c، بر اساس ساخت، و b، از b α). با تکرار استدلال های قبلی، متوجه می شویم که صفحه α شامل خطوط عمود بر صفحه β است که از خط تقاطع صفحات می گذرد. طبق تعریف، صفحات α و β عمود هستند.■

این ویژگی امکان برقراری عمود بودن هواپیماها یا اطمینان از آن را فراهم می کند.

مثال 1. سپر را طوری به پایه وصل کنید که به صورت عمودی قرار گیرد.

 اگر ستون به صورت عمودی بایستد، کافی است یک سپر به طور تصادفی به ستون وصل کنید و آن را محکم کنید (شکل 421، a). با توجه به ویژگی فوق، صفحه سپر عمود بر سطح زمین خواهد بود. در این صورت مسئله بی نهایت راه حل دارد.

اگر ستون به صورت مایل به زمین می ایستد، کافی است یک ریل عمودی به ستون وصل کنید (شکل 421، ب) و سپس سپر را به ریل و ستون وصل کنید. در این حالت، موقعیت سپر کاملاً مشخص خواهد بود، زیرا پست و ریل یک صفحه را مشخص می کنند.■

در مثال قبلی، کار "فنی" به یک مسئله ریاضی در مورد رسم یک صفحه عمود بر صفحه دیگر از طریق یک خط مستقیم داده شده کاهش یافت.

مثال 2. از راس A مربع ABCD یک قطعه AK عمود بر صفحه آن رسم می شود، AB = AK = a.

1) موقعیت نسبی هواپیماهای AKC و ABD را تعیین کنید.

AKD و ABK.

2) صفحه ای بسازید که از خط BD عمود بر صفحه ABC می گذرد.

3) صفحه ای عمود بر صفحه KAC از وسط F قطعه KC رسم کنید.

4) مساحت مثلث BDF را پیدا کنید.

 بیایید نقشه ای بسازیم که مطابق با شرایط مثال باشد (شکل 422).

1) صفحات AKC و ABD با توجه به خاصیت عمود بودن صفحات عمود هستند (قضیه 1): AK ABD بر حسب شرط. صفحات AKD و ABK نیز عمود هستند

قطبی هستند، بر اساس عمود بودن صفحات (قضیه 1). در واقع، خط AB که صفحه ABK از آن می گذرد، با توجه به علامت عمود بودن خط و صفحه، عمود بر صفحه AKD است (قضیه 1 § 18): AB AD به عنوان اضلاع مجاور مربع AB AK

AK ABD.

2) بر اساس عمود بودن صفحات، برای ساخت مورد نظر کافی است یک خط مستقیم BD در برخی نقاط رسم کنید.

408 عمود بودن خطوط و صفحات

خط عمود بر صفحه ABC و برای این کار کافی است از این نقطه خطی به موازات خط AK رسم کنید.

در واقع، طبق شرط، خط مستقیم AK بر صفحه ABC عمود است و بنابراین، طبق قضیه در مورد دو خط مستقیم موازی،

قضیه 2 (در مورد عمود بر خط تقاطع صفحات عمود بر هم).

اگر دو صفحه عمود بر هم باشند، یک خط مستقیم متعلق به یک صفحه و عمود بر تقاطع این صفحات، عمود بر صفحه دوم است.

 صفحات عمود بر هم بگذارید

α و β در امتداد خط مستقیم c قطع می شوند و خط مستقیم b در صفحه β عمود بر خط مستقیم c است و آن را در نقطه B قطع می کند (شکل 425). طبق تعریف

با تقسیم عمود بر صفحات، در صفحه β یک خط مستقیم از نقطه B می گذرد

b 1، عمود بر صفحه α. واضح است که عمود بر خط مستقیم است. اما چی-

اگر نقطه ای را روی یک خط مستقیم در یک صفحه ببرید، می توانید فقط یک خط مستقیم عمود بر خط مستقیم داده شده بکشید. از همین رو

خطوط b و b 1 منطبق هستند. این بدان معنی است که یک خط مستقیم از یک صفحه، عمود بر خط تقاطع دو صفحه عمود بر صفحه دوم، عمود بر صفحه دوم است. ■

اجازه دهید قضیه در نظر گرفته شده را برای اثبات علامت دیگری از عمود بودن صفحات، که از نقطه نظر مطالعه بعدی موقعیت نسبی دو صفحه مهم است، اعمال کنیم.

اجازه دهید صفحات α و β عمود بر هم باشند، خط مستقیم c خط تقاطع آنها است. از طریق نقطه دلخواه A یک خط مستقیم c می کشیم

در صفحات α و β، خطوط مستقیم a و b، عمود بر خطوط مستقیم c (شکل 426). طبق نظریه

Me 2، خطوط مستقیم a و b به ترتیب عمود بر صفحات β و α هستند، بنابراین آنها بر یکدیگر عمود هستند: a b . سر راست

a و b تعریف شده سطح مشخص γ را تعریف می کنند. خط تقاطع با صفحات α و β

عمود بر صفحه γ، بر اساس عمود بودن خط و صفحه (قضیه 1 § 18): c a, c b, a γ, b γ. اگر خودسری انتخاب نقطه A روی خط مستقیم c و اینکه تنها صفحه عمود بر آن از نقطه A خط مستقیم می گذرد را در نظر بگیریم، می توانیم نتیجه زیر را بگیریم.

قضیه 3 (در مورد صفحه عمود بر خط تقاطع صفحات عمود بر هم).

صفحه ای عمود بر خط تقاطع دو صفحه عمود بر هم این صفحات را در امتداد خطوط مستقیم عمود بر هم قطع می کند.

بنابراین، یک ویژگی دیگر از صفحات عمود بر هم ایجاد شده است. این خاصیت مشخصه است، یعنی اگر برای چند صفحه صادق باشد، صفحات بر هم عمود هستند. ما یک علامت دیگر از عمود بودن صفحات داریم.

قضیه 4 (معیار دوم برای عمود بودن صفحات).

اگر تقاطع مستقیم دو صفحه با صفحه سوم عمود بر خط تقاطع آنها عمود باشد، این صفحات نیز عمود هستند.

اجازه دهید صفحات α و β در امتداد خط مستقیم س و صفحه γ، عمود بر خط مستقیم س، صفحات α و β را به ترتیب قطع کند.

به ترتیب در امتداد خطوط مستقیم a و b (شکل 427). با شرط، a b. از آنجایی که γc، سپس c. و بنابراین با توجه به علامت عمود بودن خط و صفحه، خط بر صفحه β عمود است (قضیه 1 § 18). خودشه-

بله، این نتیجه می شود که صفحات α و β بر اساس علامت عمود بودن صفحات، عمود هستند (قضیه 1).■

همچنین قضایایی در مورد اتصالات بین عمود بودن دو صفحه از صفحه سوم و موقعیت متقابل آنها قابل توجه است.

قضیه 5 (در مورد خط تقاطع دو صفحه عمود بر صفحه سوم).

اگر دو صفحه عمود بر صفحه سوم همدیگر را قطع کنند، خط تقاطع آنها بر این صفحه عمود است.

اجازه دهید صفحات α و β، عمود بر صفحه γ، در امتداد یک خط مستقیم قطع شوند (a || γ)، و A نقطه تلاقی خط مستقیم با

اجازه دهید یک قضیه را در نظر بگیریم که رابطه بین موازی بودن و عمود بودن صفحات را توصیف می کند. ما قبلاً نتیجه مربوطه را برای خطوط مستقیم و صفحات داشتیم.

قضیه 6 (در مورد صفحات موازی عمود بر صفحه سوم).

اگر یکی از دو صفحه موازی بر صفحه سوم عمود باشد، صفحه دوم بر آن عمود است.

فرض کنید صفحات α و β موازی باشند و صفحه γ عمود بر صفحه α باشند. از آنجایی که هواپیما γ

صفحه α را قطع می کند، سپس باید صفحه β را به موازات آن قطع کند. بیایید یک طرفدار بگیریم

یک خط مستقیم دلخواه m عمود بر صفحه γ و از طریق آن، و همچنین از طریق یک نقطه دلخواه از صفحه β، صفحه δ را بکشید (شکل 429).

صفحات δ و β در امتداد یک خط مستقیم n قطع می شوند و از آنجایی که α║ β، پس از آن ║ n هستند (قضیه 2 §18). از قضیه 1 نتیجه می گیرد که γ و بنابراین صفحه β که از خط مستقیم می گذرد نیز بر صفحه γ عمود خواهد بود. ■

قضیه اثبات شده نشانه دیگری از عمود بودن صفحات می دهد.

می توانید با استفاده از علامت عمود بودن صفحات یک صفحه عمود بر نقطه داده شده را از طریق یک نقطه معین رسم کنید (قضیه 1). کافی است یک خط مستقیم از طریق این نقطه عمود بر صفحه داده شده رسم کنید (مسئله 1 § 19 را ببینید). و سپس یک صفحه را از طریق خط مستقیم ساخته شده با توجه به معیار مشخص شده عمود خواهد کرد. واضح است که بی نهایت از این هواپیماها را می توان ترسیم کرد.

معنی دارتر مسئله ساختن صفحه ای عمود بر یک صفحه معین است، مشروط بر اینکه از یک خط معین عبور کند. واضح است که اگر یک خط معین بر یک صفحه معین عمود باشد، می توان تعداد نامحدودی از این صفحات را ساخت. در نظر گرفتن این مورد باقی می ماند که خط داده شده عمود بر صفحه داده شده نباشد. امکان چنین ساخت و ساز در سطح مدل های فیزیکی خطوط مستقیم و سطوح در مثال 1 توجیه شده است.

وظیفه 1. ثابت کنید که از طریق یک خط دلخواه غیر عمود بر یک صفحه، می توان صفحه ای عمود بر صفحه داده شده رسم کرد.

 یک صفحه α و یک خط l، l B\ a داده شود. بیایید یک نقطه دلخواه M را روی یک خط مستقیم بگیریم و یک خط مستقیم از آن، عمود بر صفحه α بکشیم (شکل 430، a). از آنجایی که طبق شرط، l عمود بر α نیست، پس خطوط l آن را قطع می کنند. از طریق این خطوط مستقیم می توان صفحه β را رسم کرد (شکل 430، ب) که با توجه به آزمایش عمود بودن صفحات (قضیه 1) بر صفحه α عمود خواهد بود. ■

مثال 3. از طریق رأس A هرم منظم SABC با پایه ABC، یک خط مستقیم عمود بر صفحه وجه جانبی SBC بکشید.

 برای حل این مشکل از قضیه عمود بر خط تقاطع صفحات عمود استفاده می کنیم.

(قضیه 2). بگذارید K نقطه وسط لبه BC باشد (شکل 431). صفحات AKS و BCS با توجه به علامت عمود بودن صفحات (قضیه 1) عمود هستند. در واقع، BC SK و BC AK مانند میانه هایی هستند که به سمت قاعده های مثلث متساوی الساقین کشیده شده اند. بنابراین، با توجه به معیار عمود بودن یک خط و یک صفحه (قضیه 1 §18)، خط BC بر صفحه AKS عمود است. صفحه BCS از خطی عمود بر صفحه AKS می گذرد.

ساخت و ساز. اجازه دهید یک خط AL در صفحه AKS از نقطه A، عمود بر خط KS بکشیم - خط تقاطع هواپیماهای AKS و BCS (شکل 432). با قضیه عمود بر خط تقاطع صفحات عمود بر هم (قضیه 2)، خط AL بر صفحه BCS عمود است. ■

2. در شکل 434 به درستی نشان داده شده است- هرم چهار گوش جدید

SABCD، نقاط P، M، N - وسط -

ما لبه های AB، BC، BS، O داریم - مرکز پایه ABCD. کدام یک از جفت ها صاف هستند- استخوان ها عمود هستند:

1) ACS و BDS 2) MOS و POS.

3) COS و MNP؛ 4) MNP و SOB.

5) CND و ABS؟

3) PAC و PBC. 4) PAC و PAB؟

4. این دو صفحه عمود بر هم هستند. آیا ممکن است از طریق یک نقطه دلخواه یکی ازآیا باید یک خط مستقیم در این صفحه، صفحه دوم بکشند؟

5. کشیدن یک خط مستقیم در صفحه α غیرممکن است، اما در صفحه β. آیا این هواپیماها می توانند مای باشند؟

6. آیا از نقطه معینی از صفحه α خطی در این صفحه می گذرد و عمود بر صفحه است، به طوری که صفحات α و β عمود بر هم باشند؟

قسمتی از نرده به یک تیر عمودی متصل است، آیا می توان ادعا کرد که صفحه نرده عمودی است؟

چگونه یک سپر را به صورت عمودی به یک ریل موازی با سطح زمین وصل کنیم؟

چرا سطح درها، صرف نظر از بسته یا باز بودن، نسبت به زمین عمودی است؟

چرا یک شاقول محکم روی یک دیوار عمودی قرار می گیرد، اما نه لزوماً روی دیوار شیبدار؟

آیا می توان سپر را به یک ستون شیبدار وصل کرد که عمود بر سطح زمین باشد؟

چگونه عملاً تعیین کنیم که آیا یک صفحه عمود است؟

دیوارها کف هواپیما؟ عمود برپاندیکول عمود- مستقیم، دراز کشیده - β. درست 7. . ممکن است 8.9.10.11.12.

تمرین های گرافیکی

1. در شکل 436 یک مکعب را نشان می دهد ABCDA 1 B 1 C 1 D 1 .

1) صفحات عمود بر صفحه را مشخص کنید VDD 1.

2) هواپیماها چطوره و

A1 B1 CAB 1 C 1

421. پاره OS از مرکز O مربع ABCD عمود بر صفحه آن رسم می شود.

1°) موقعیت نسبی صفحات ACS را تعیین کنید

و ABC.

2 درجه) موقعیت نسبی صفحات ACS را تعیین کنید

و BDS.

3) صفحه ای بسازید که از خط OS عمود بر صفحه ABS عبور می کند.

4) صفحه ای عمود بر صفحه ABC بسازید که از وسط اضلاع AD و CD می گذرد.

422. از نقطه تقاطع O مورب های لوزی ABCD، یک قطعه OS عمود بر صفحه لوزی رسم می شود

1°) موقعیت نسبی SDB را تعیین کنید و

ABC، SDB و ACS.

2°) صفحه ای بسازید که از خط BC عمود بر صفحه ABD می گذرد.

3) صفحه ای عمود بر صفحه ABC از وسط F قطعه CS رسم کنید.

4) مساحت مثلث BDF را پیدا کنید.

423. یک مکعب ABCDA1 B1 C1 D1 داده می شود.

1°) موقعیت نسبی صفحات AB 1 C 1 را تعیین کنید

و CDD1.

2°) موقعیت نسبی صفحات AB 1 C 1 را تعیین کنید

و CD1 A1.

3 درجه) صفحه ای بسازید که از نقطه A عمود بر صفحه BB 1 D 1 می گذرد.

4) قسمتی از مکعب را با صفحه ای بسازید که از وسط یال های A 1 D 1 و B 1 C 1 عمود بر صفحه ABC می گذرد. 5) موقعیت نسبی صفحه AA 1 B و صفحه ای که از وسط دنده های A 1 B 1 , C 1 D 1 , CD می گذرد را تعیین کنید.

6) سطح مقطع مکعب را با صفحه ای که از لبه BB 1 و وسط لبه A 1 D 1 می گذرد (BB 1 = a) پیدا کنید.

7) یک نقطه متقارن به نقطه A نسبت به صفحه A 1 B 1 C بسازید.

424. در چهار وجهی منظم ABCD با لبه 2 سانتی متر نقطه M وسط DB و نقطه N وسط AC است.

1 درجه) ثابت کنید که خط مستقیم DB بر صفحه عمود است

2°) ثابت کنید که صفحه BDM عمود بر صفحه AMC است.

3) از طریق نقطه O تقاطع وسط مثلث ADC یک خط مستقیم عمود بر صفحه AMC بکشید.

4) طول این پاره خط را در داخل چهار وجهی بیابید. 5) صفحه AMC این بخش را به چه نسبتی تقسیم می کند؟

425. دو مثلث متساوی الاضلاع ABC و ADC در صفحات عمود بر هم قرار دارند.

1°) طول قطعه BD را در صورتی که AC = 1 سانتی متر باشد، بیابید.

2) ثابت کنید که صفحه BKD (K روی خط AC قرار دارد) بر صفحه هر یک از مثلث ها عمود است اگر و فقط اگر K نقطه وسط ضلع AC باشد.

426. مستطیل ABCD که اضلاع آن 3 سانتی متر و 4 سانتی متر است در امتداد AC مورب خم شد به طوری که مثلث های ABC و ADC در صفحات عمود بر هم قرار گرفتند. فاصله بین نقاط B و D را پس از خم کردن مستطیل ABCD تعیین کنید.

427. از این نقطه یک صفحه عمود بر هر یک از دو صفحه داده شده بکشید.

428 درجه ثابت کنید که صفحات مجاور یک مکعب عمود هستند.

429. صفحات α و β بر هم عمود هستند. از نقطه A صفحه α، یک خط مستقیم AB عمود بر صفحه β رسم می شود. ثابت کنید که خط AB در صفحه α قرار دارد.

430- ثابت كنيد كه اگر صفحه و خطي كه در اين صفحه قرار ندارند بر يك صفحه عمود باشند پس با هم موازي هستند.

431. از طریق نقاط A و B که روی خط تقاطع صفحات α و β عمود بر یکدیگر قرار دارند، خطوط مستقیم عمود بر هم کشیده می شوند: AA 1 در α، BB 1 در β. نقطه X روی خط AA 1 و نقطه Y روی BB 1 قرار دارد. ثابت کنید که خط مستقیم ВB 1 بر خط مستقیم ВХ عمود است و خط مستقیم АА 1 بر خط مستقیم АY عمود است.

432*. از وسط هر ضلع مثلث، صفحه ای عمود بر این ضلع کشیده شده است. ثابت کنید که هر سه صفحه ترسیم شده در امتداد یک خط مستقیم عمود بر صفحه مثلث همدیگر را قطع می کنند.

تمرین هایی برای تکرار

433. در مثلث متساوی الاضلاع با ضلعب تعیین: 1) ارتفاع. 2) شعاع دایره های محاطی و محاطی.

434. از یک نقطه یک خط عمود و دو خط مورب به یک خط معین رسم می شود. اگر عمودهای مایل 41 سانتی متر و 50 سانتی متر باشند و برآمدگی آنها روی این خط به نسبت 3:10 باشد، طول عمود را تعیین کنید.

435. ساق های مثلث قائم الزاویه اگر bis را تعیین کنید- مقاطع یک زاویه قائمه، هیپوتنوس را به قطعات 15 سانتی متری تقسیم می کند و

تعریف پایه

دو هواپیما نامیده می شوند

عمود هستند ، اگر هر یک از آنها توسط خطوط مستقیم تشکیل شده باشد- مایل، عمود بر- مایل از صفحه دوم و عبور از نقاط تقاطع این صفحات.

مفهوم صفحات عمود بر هم

وقتی دو صفحه با هم تلاقی می کنند، زوایای دو وجهی 4 دلاری به دست می آید. دو زاویه برابر با $\varphi $ و دو زاویه دیگر برابر با $(180)^0-\varphi $ هستند.

تعریف 1

زاویه بین صفحات حداقل زوایای دو وجهی تشکیل شده توسط این صفحات است.

تعریف 2

اگر زاویه بین این صفحات 90$^\circ$ باشد، دو صفحه متقاطع عمود نامیده می شوند (شکل 1).

شکل 1. صفحات عمود بر هم

علامت عمود بودن دو صفحه

قضیه 1

اگر یک خط مستقیم از یک صفحه بر صفحه دیگر عمود باشد، آنگاه این صفحات بر یکدیگر عمود هستند.

اثبات

اجازه دهید صفحات $\alpha $ و $\beta $، که در امتداد خط مستقیم $AC$ قطع می شوند، به ما داده شود. بگذارید خط مستقیم $AB$ واقع در صفحه $\alpha $ عمود بر صفحه $\beta $ باشد (شکل 2).

شکل 2.

از آنجایی که خط $AB$ بر صفحه $\beta$ عمود است، بر خط $AC$ نیز عمود است. اجازه دهید علاوه بر این یک خط $AD$ در صفحه $\beta$، عمود بر خط $AC$ رسم کنیم.

متوجه شدیم که زاویه $BAD$ زاویه خطی زاویه دو وجهی است که برابر با $90^\circ$ است. یعنی طبق تعریف 1، زاویه بین صفحات 90$^\circ$ است، یعنی این صفحات عمود هستند.

قضیه ثابت شده است.

از این قضیه قضیه زیر حاصل می شود.

قضیه 2

اگر صفحه ای عمود بر خطی باشد که دو صفحه دیگر در امتداد آن تلاقی می کنند، آن صفحه نیز عمود بر این صفحات است.

اثبات

اجازه دهید دو صفحه $\alpha $ و $\beta $ در امتداد خط مستقیم $c$ به ما داده شود. صفحه $\gamma $ عمود بر خط مستقیم $c$ است (شکل 3)

شکل 3.

از آنجایی که خط $c$ متعلق به صفحه $\alpha $ و صفحه $\gamma $ عمود بر خط $c$ است، پس طبق قضیه 1، صفحات $\alpha $ و $\gamma $ عمود هستند.

از آنجایی که خط $c$ متعلق به صفحه $\beta $ است و صفحه $\gamma $ عمود بر خط $c$ است، پس طبق قضیه 1، صفحات $\beta $ و $\gamma $ عمود هستند.

قضیه ثابت شده است.

برای هر یک از این قضایا، گزاره های معکوس نیز صادق هستند.

نمونه هایی از مشکلات

مثال 1

اجازه دهید یک متوازی الاضلاع مستطیلی $ABCDA_1B_1C_1D_1$ به ما داده شود. تمام جفت صفحات عمود بر هم را پیدا کنید (شکل 5).

شکل 4.

راه حل.

با تعریف صفحات متوازی الاضلاع و عمود بر مستطیل، هشت جفت صفحه زیر را عمود بر یکدیگر می بینیم: $(ABB_1)$ و $(ADD_1)$، $(ABB_1)$ و $(A_1B_1C_1)$، $( ABB_1)$ و $(BCC_1) $، $(ABB_1)$ و $(ABC)$، $(DCC_1)$ و $(ADD_1)$، $(DCC_1)$ و $(A_1B_1C_1)$، $(DCC_1) $ و $(BCC_1)$، $(DCC_1)$ و $(ABC)$.

مثال 2

اجازه دهید دو صفحه عمود بر هم به ما داده شود. از یک نقطه در یک صفحه یک عمود بر صفحه دیگر کشیده می شود. ثابت کنید که این خط در صفحه داده شده قرار دارد.

اثبات

اجازه دهید صفحات عمودی $\alpha $ و $\beta $ را که در امتداد خط مستقیم $c$ متقاطع هستند به ما داده شود. از نقطه $A$ صفحه $\beta $ یک $AC$ عمود بر صفحه $\alpha $ کشیده می شود. اجازه دهید فرض کنیم که $AC$ در صفحه $\beta$ قرار ندارد (شکل 6).

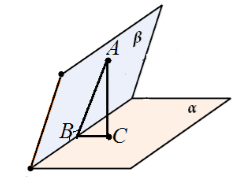
شکل 5.

مثلث $ABC$ را در نظر بگیرید. مستطیل شکل با زاویه راست $ACB$ است. بنابراین، $\angle ABC\ne (90)^0$.

اما از سوی دیگر، $\angle ABC$ زاویه خطی زاویه دو وجهی است که توسط این صفحات تشکیل شده است. یعنی زاویه دو وجهی تشکیل شده توسط این صفحات برابر با 90 درجه نیست. متوجه شدیم که زاویه بین صفحات برابر با $90^\circ$ نیست. تناقض. بنابراین، $AC$ در صفحه $\beta$ قرار دارد.