Что такое параллелограмм и его свойства. Исследовательский проект "параллелограмм и его свойства"

Параллелограмм представляет собой четырехугольник, у которого противоположные стороны попарно параллельны. Это определение уже достаточно, так как остальные свойства параллелограмма следуют из него и доказываются в виде теорем.

Основными свойствами параллелограмма являются:

параллелограмм - это выпуклый четырехугольник;
у параллелограмма противоположные стороны попарно равны;
у параллелограмма противоположные углы попарно равны;
диагонали параллелограмма точкой пересечения делятся пополам.

Параллелограмм - выпуклый четырехугольник

Докажем сначала теорему о том, что параллелограмм является выпуклым четырехугольником . Многоугольник является выпуклым тогда, когда какая бы его сторона не была продлена до прямой, все остальные стороны многоугольника окажутся по одну сторону от этой прямой.

Пусть дан параллелограмм ABCD, у которого AB противоположная сторона для CD, а BC - противоположная для AD. Тогда из определения параллелограмма следует, что AB || CD, BC || AD.

У параллельных отрезков нет общих точек, они не пересекаются. Это значит, что CD лежит по одну сторону от AB. Поскольку отрезок BC соединяет точку B отрезка AB с точкой C отрезка CD, а отрезок AD соединяет другие точки AB и CD, то отрезки BC и AD также лежат по ту же сторону от прямой AB, где лежит CD. Таким образом, все три стороны - CD, BC, AD - лежат по одну сторону от AB.

Аналогично доказывается, что по отношению к другим сторонам параллелограмма три остальные стороны лежат с одной стороны.

Противоположные стороны и углы равны

Одним из свойств параллелограмма является то, что в параллелограмме противоположные стороны и противоположные углы попарно равны . Например, если дан параллелограмм ABCD, то у него AB = CD, AD = BC, ∠A = ∠C, ∠B = ∠D. Доказывается эта теорема следующим образом.

Параллелограмм является четырехугольником. Значит, у него две диагонали. Так как параллелограмм - это выпуклый четырехугольник, то любая из них делит его на два треугольника. Рассмотрим в параллелограмме ABCD треугольники ABC и ADC, полученные в результате проведения диагонали AC.

У этих треугольников одна сторона общая - AC. Угол BCA равен углу CAD, как вертикальные при параллельных BC и AD. Углы BAC и ACD также равны как вертикальные при параллельных AB и CD. Следовательно, ∆ABC = ∆ADC по двум углам и стороне между ними.

В этих треугольниках стороне AB соответствует сторона CD, а стороне BC соответствует AD. Следовательно, AB = CD и BC = AD.

Углу B соответствует угол D, т. е. ∠B = ∠D. Угол A параллелограмма представляет собой сумму двух углов - ∠BAC и ∠CAD. Угол же C равен состоит из ∠BCA и ∠ACD. Так как пары углов равны друг другу, то ∠A = ∠C.

Таким образом, доказано, что в параллелограмме противоположные стороны и углы равны.

Диагонали делятся пополам

Так как параллелограмм - это выпуклый четырехугольник, то у него две две диагонали, и они пересекаются. Пусть дан параллелограмм ABCD, его диагонали AC и BD пересекаются в точке E. Рассмотрим образованные ими треугольники ABE и CDE.

У этих треугольников стороны AB и CD равны как противоположные стороны параллелограмма. Угол ABE равен углу CDE как накрест лежащие при параллельных прямых AB и CD. По этой же причине ∠BAE = ∠DCE. Значит, ∆ABE = ∆CDE по двум углам и стороне между ними.

Также можно заметить, что углы AEB и CED вертикальные, а следовательно, тоже равны друг другу.

Так как треугольники ABE и CDE равны друг другу, то равны и все их соответствующие элементы. Стороне AE первого треугольника соответствует сторона CE второго, значит, AE = CE. Аналогично BE = DE. Каждая пара равных отрезков составляет диагональ параллелограмма. Таким образом доказано, что диагонали параллелограмма делятся точкой пересечения пополам .

При-зна-ки па-рал-ле-ло-грам-ма

1. Определение и основные свойства параллелограмма

Нач-нем с того, что вспом-ним опре-де-ле-ние па-рал-ле-ло-грам-ма.

Опре-де-ле-ние. Па-рал-ле-ло-грамм - че-ты-рех-уголь-ник, у ко-то-ро-го каж-дые две про-ти-во-по-лож-ные сто-ро-ны па-рал-лель-ны (см. Рис. 1).

Рис. 1. Па-рал-ле-ло-грамм

Вспом-ним ос-нов-ные свой-ства па-рал-ле-ло-грам-ма :

Для того, чтобы иметь воз-мож-ность поль-зо-вать-ся всеми этими свой-ства-ми, необ-хо-ди-мо быть уве-рен-ным, что фи-гу-ра, о ко-то-рой идет речь, - па-рал-ле-ло-грамм. Для этого необ-хо-ди-мо знать такие факты, как при-зна-ки па-рал-ле-ло-грам-ма. Пер-вые два из них мы се-год-ня и рас-смот-рим.

2. Первый признак параллелограмма

Тео-ре-ма. Пер-вый при-знак па-рал-ле-ло-грам-ма. Если в че-ты-рех-уголь-ни-ке две про-ти-во-по-лож-ные сто-ро-ны равны и па-рал-лель-ны, то этот че-ты-рех-уголь-ник - па-рал-ле-ло-грамм . .

Рис. 2. Пер-вый при-знак па-рал-ле-ло-грам-ма

До-ка-за-тель-ство. Про-ве-дем в че-ты-рех-уголь-ни-ке диа-го-наль (см. Рис. 2), она раз-би-ла его на два тре-уголь-ни-ка. За-пи-шем, что мы знаем об этих тре-уголь-ни-ках:

по пер-во-му при-зна-ку ра-вен-ства тре-уголь-ни-ков.

Из ра-вен-ства ука-зан-ных тре-уголь-ни-ков сле-ду-ет, что по при-зна-ку па-рал-лель-но-сти пря-мых при пе-ре-се-че-нии их се-ку-щей. Имеем, что:

До-ка-за-но.

3. Второй признак параллелограмма

Тео-ре-ма. Вто-рой при-знак па-рал-ле-ло-грам-ма. Если в че-ты-рех-уголь-ни-ке каж-дые две про-ти-во-по-лож-ные сто-ро-ны равны, то этот че-ты-рех-уголь-ник - па-рал-ле-ло-грамм . .

Рис. 3. Вто-рой при-знак па-рал-ле-ло-грам-ма

До-ка-за-тель-ство. Про-ве-дем в че-ты-рех-уголь-ни-ке диа-го-наль (см. Рис. 3), она раз-би-ва-ет его на два тре-уголь-ни-ка. За-пи-шем, что мы знаем об этих тре-уголь-ни-ках, ис-хо-дя из фор-му-ли-ров-ки тео-ре-мы:

по тре-тье-му при-зна-ку ра-вен-ства тре-уголь-ни-ков.

Из ра-вен-ства тре-уголь-ни-ков сле-ду-ет, что и по при-зна-ку па-рал-лель-но-сти пря-мых при пе-ре-се-че-нии их се-ку-щей. По-лу-ча-ем:

па-рал-ле-ло-грамм по опре-де-ле-нию. Что и тре-бо-ва-лось до-ка-зать.

До-ка-за-но.

4. Пример на применение первого признака параллелограмма

Рас-смот-рим при-мер на при-ме-не-ние при-зна-ков па-рал-ле-ло-грам-ма.

При-мер 1. В вы-пук-лом че-ты-рех-уголь-ни-ке Найти: а) углы че-ты-рех-уголь-ни-ка; б) сто-ро-ну .

Ре-ше-ние. Изоб-ра-зим Рис. 4.

па-рал-ле-ло-грамм по пер-во-му при-зна-ку па-рал-ле-ло-грам-ма.

А. по свой-ству па-рал-ле-ло-грам-ма о про-ти-во-по-лож-ных углах, по свой-ству па-рал-ле-ло-грам-ма о сумме углов, при-ле-жа-щих к одной сто-роне.

Б. по свой-ству ра-вен-ства про-ти-во-по-лож-ных сто-рон.

ре-тий при-знак па-рал-ле-ло-грам-ма

5. Повторение: определение и свойства параллелограмма

На-пом-ним, что па-рал-ле-ло-грамм - это че-ты-рёх-уголь-ник, у ко-то-ро-го про-ти-во-по-лож-ные сто-ро-ны по-пар-но па-рал-лель-ны. То есть, если - па-рал-ле-ло-грамм, то (см. Рис. 1).

Па-рал-ле-ло-грамм об-ла-да-ет целым рядом свойств: про-ти-во-по-лож-ные углы равны (), про-ти-во-по-лож-ные сто-ро-ны равны (). Кроме того, диа-го-на-ли па-рал-ле-ло-грам-ма в точке пе-ре-се-че-ния де-лят-ся по-по-лам, сумма углов, при-ле-жа-щих к любой сто-роне па-рал-ле-ло-грам-ма, равна и т.д.

Но для того, чтобы поль-зо-вать-ся всеми этими свой-ства-ми, необ-хо-ди-мо быть аб-со-лют-но уве-рен-ны-ми в том, что рас-смат-ри-ва-е-мый че-ты-рёх-уголь-ник - па-рал-ле-ло-грамм. Для этого и су-ще-ству-ют при-зна-ки па-рал-ле-ло-грам-ма: то есть те факты, из ко-то-рых можно сде-лать од-но-знач-ный вывод, что че-ты-рёх-уголь-ник яв-ля-ет-ся па-рал-ле-ло-грам-мом. На преды-ду-щем уроке мы уже рас-смот-ре-ли два при-зна-ка. Сей-час рас-смот-рим тре-тий.

6. Третий признак параллелограмма и его доказательство

Если в че-ты-рёх-уголь-ни-ке диа-го-на-ли в точке пе-ре-се-че-ния де-лят-ся по-по-лам, то дан-ный че-ты-рёх-уголь-ник яв-ля-ет-ся па-рал-ле-ло-грам-мом.

Дано:

Че-ты-рёх-уголь-ник; ; .

До-ка-зать:

Па-рал-ле-ло-грамм.

До-ка-за-тель-ство:

Для того чтобы до-ка-зать дан-ный факт, необ-хо-ди-мо до-ка-зать па-рал-лель-ность сто-рон па-рал-ле-ло-грам-ма. А па-рал-лель-ность пря-мых чаще всего до-ка-зы-ва-ет-ся через ра-вен-ство внут-рен-них на-крест ле-жа-щих углов при этих пря-мых. Таким об-ра-зом, на-пра-ши-ва-ет-ся сле-ду-ю-щий спо-соб до-ка-за-тель-ства тре-тье-го при-зна-ка па-рал-ле-ло-грам-ма: через ра-вен-ство тре-уголь-ни-ков .

До-ка-жем ра-вен-ство этих тре-уголь-ни-ков. Дей-стви-тель-но, из усло-вия сле-ду-ет: . Кроме того, по-сколь-ку углы - вер-ти-каль-ные, то они равны. То есть:

(пер-вый при-знак ра-вен-ства тре-уголь-ни-ков - по двум сто-ро-нам и углу между ними).

Из ра-вен-ства тре-уголь-ни-ков: (так как равны внут-рен-ние на-крест ле-жа-щие углы при этих пря-мых и се-ку-щей ). Кроме того, из ра-вен-ства тре-уголь-ни-ков сле-ду-ет, что . Зна-чит, мы по-лу-чи-ли, что в че-ты-рёх-уголь-ни-ке две сто-ро-ны равны и па-рал-лель-ны. По пер-во-му при-зна-ку па-рал-ле-ло-грам-ма: - па-рал-ле-ло-грамм.

До-ка-за-но.

7. Пример задачи на третий признак параллелограмма и обобщение

Рас-смот-рим при-мер на при-ме-не-ние тре-тье-го при-зна-ка па-рал-ле-ло-грам-ма.

При-мер 1

Дано:

- па-рал-ле-ло-грамм; . - се-ре-ди-на , - се-ре-ди-на , - се-ре-ди-на , - се-ре-ди-на (см. Рис. 2).

До-ка-зать: - па-рал-ле-ло-грамм.

До-ка-за-тель-ство:

Зна-чит, в че-ты-рёх-уголь-ни-ке диа-го-на-ли в точке пе-ре-се-че-ния де-лят-ся по-по-лам. По тре-тье-му при-зна-ку па-рал-ле-ло-грам-ма из этого сле-ду-ет, что - па-рал-ле-ло-грамм.

До-ка-за-но.

Если про-ве-сти ана-лиз тре-тье-го при-зна-ка па-рал-ле-ло-грам-ма, то можно за-ме-тить, что этот при-знак со-от-вет-ству-ет свой-ству па-рал-ле-ло-грам-ма. То есть, то, что диа-го-на-ли де-лят-ся по-по-лам, яв-ля-ет-ся не про-сто свой-ством па-рал-ле-ло-грам-ма, а его от-ли-чи-тель-ным, ха-рак-те-ри-сти-че-ским свой-ством, по ко-то-ро-му его можно вы-де-лить из мно-же-ства че-ты-рёх-уголь-ни-ков.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/priznaki-parallelogramma

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/tretiy-priznak-parallelogramma

http://www.uchportfolio.ru/users_content/675f9820626f5bc0afb47b57890b466e/images/46TThxQ8j4Y.jpg

http://cs10002.vk.me/u31195134/116260458/x_56d40dd3.jpg

http://wwww.tepka.ru/geometriya/16.1.gif

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля - до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

Понятие параллелограмма

Определение 1

Параллелограмм -- это четырехугольник, в котором противоположные стороны параллельны между собой (рис. 1).

Рисунок 1.

Параллелограмм имеет два основных свойства. Рассмотрим их без доказательства.

Свойство 1: Противоположные стороны и углы параллелограмма равны, соответственно, между собой.

Свойство 2: Диагонали, проведенные в параллелограмме, делятся пополам их точкой пересечения.

Признаки параллелограмма

Рассмотрим три признака параллелограмма и представим их в виде теорем.

Теорема 1

Если две стороны четырехугольника равны между собой, а также параллельны, то этот четырехугольник будет параллелограммом.

Доказательство.

Пусть нам дан четырехугольник $ABCD$. В котором $AB||CD$ и $AB=CD$ Проведем в нем диагональ $AC$ (рис. 2).

Рисунок 2.

Рассмотрим параллельные прямые $AB$ и $CD$ и их секущую $AC$. Тогда

\[\angle CAB=\angle DCA\]

как накрест лежащие углы.

По $I$ признаку равенства треугольников,

так как $AC$ -- их общая сторона, а $AB=CD$ по условию. Значит

\[\angle DAC=\angle ACB\]

Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$.}Следовательно, по определению $1$, данный четырехугольник является параллелограммом.

Теорема доказана.

Теорема 2

Если противоположные стороны четырехугольника равны между собой, то он является параллелограммом.

Доказательство.

Пусть нам дан четырехугольник $ABCD$. В котором $AD=BC$ и $AB=CD$. Проведем в нем диагональ $AC$ (рис. 3).

Рисунок 3.

Так как $AD=BC$, $AB=CD$, а $AC$ -- общая сторона, то по $III$ признаку равенства треугольников,

\[\triangle DAC=\triangle ACB\]

\[\angle DAC=\angle ACB\]

Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$. Следовательно, по определению $1$, данный четырехугольник является параллелограммом.

\[\angle DCA=\angle CAB\]

Рассмотрим прямые $AB$ и $CD$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AB||CD$. Следовательно, по определению 1, данный четырехугольник является параллелограммом.

Теорема доказана.

Теорема 3

Если диагонали, проведенные в четырехугольнике, своей точкой пересечения делятся на две равные части, то этот четырехугольник является параллелограммом.

Доказательство.

Пусть нам дан четырехугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $O$ (рис. 4).

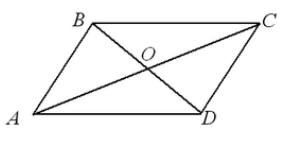
Рисунок 4.

Так как, по условию $BO=OD,\ AO=OC$, а углы $\angle COB=\angle DOA$ как вертикальные, то, по $I$ признаку равенства треугольников,

\[\triangle BOC=\triangle AOD\]

\[\angle DBC=\angle BDA\]

Рассмотрим прямые $BC$ и $AD$ и их секущую $BD$, по последнему равенству накрест лежащих углов получим, что $BC||AD$. Также $BC=AD$. Следовательно, по теореме $1$, данный четырехугольник является параллелограммом.