The cross product of vectors in two-dimensional space. Vector product of vectors online. Establishing collinearity of vectors

This online calculator calculates the vector product of vectors. A detailed solution is given. To calculate the cross product of vectors, enter the coordinates of the vectors in the cells and click on the "Calculate" button.

×

Warning

Clear all cells?

Close Clear

Data entry instructions. Numbers are entered as integers (examples: 487, 5, -7623, etc.), decimals (ex. 67., 102.54, etc.) or fractions. The fraction must be entered in the form a/b, where a and b (b>0) are integers or decimals. Examples 45/5, 6.6/76.4, -7/6.7, etc.

Vector product of vectors

Before moving on to the definition of the vector product of vectors, let's consider the concepts ordered vector triplet, left vector triplet, right vector triplet.

Definition 1. Three vectors are called ordered triple(or triple), if it is indicated which of these vectors is the first, which is the second and which is the third.

Record cba- means - the first is a vector c, the second is the vector b and the third is the vector a.

Definition 2. Triple of non-coplanar vectors abc is called right (left) if, when reduced to a common origin, these vectors are located in the same way as the large, unbent index and middle fingers of the right (left) hand are located, respectively.

Definition 2 can be formulated differently.

Definition 2". Triple of non-coplanar vectors abc is called right (left) if, when reduced to a common origin, the vector c is located on the other side of the plane defined by the vectors a And b, where is the shortest turn from a To b performed counterclockwise (clockwise).

Troika of vectors abc, shown in Fig. 1 is right, and three abc shown in Fig. 2 is the left one.

If two triplets of vectors are right or left, then they are said to be of the same orientation. Otherwise they are said to be of opposite orientation.

Definition 3. A Cartesian or affine coordinate system is called right (left) if three basis vectors form a right (left) triple.

For definiteness, in what follows we will consider only right-handed coordinate systems.

Definition 4. Vector artwork vector a to vector b called a vector With, denoted by the symbol c=[ab] (or c=[a,b], or c=a×b) and satisfying the following three requirements:

• vector length With equal to the product of vector lengths a And b by the sine of the angle φ between them:

|c|=|[ab]|=|a||b|sinφ;

(1)

• vector With orthogonal to each of the vectors a And b;
• vector c directed so that the three abc is right.

The cross product of vectors has the following properties:

• [ab]=−[ba] (anti-permutability factors);
• [(λa)b]=λ [ab] (combination relative to the numerical factor);
• [(a+b)c]=[ac]+[bc] (distributiveness relative to the sum of vectors);
• [aa]=0 for any vector a.

Geometric properties of the vector product of vectors

Theorem 1. For two vectors to be collinear, it is necessary and sufficient that their vector product be equal to zero.

Proof. Necessity. Let the vectors a And b collinear. Then the angle between them is 0 or 180° and sinφ=sin180=sin 0=0. Therefore, taking into account expression (1), the length of the vector c equal to zero. Then c zero vector.

Adequacy. Let the vector product of vectors a And b obviously zero: [ ab]=0. Let us prove that the vectors a And b collinear. If at least one of the vectors a And b zero, then these vectors are collinear (since the zero vector has an indefinite direction and can be considered collinear to any vector).

If both vectors a And b non-zero, then | a|>0, |b|>0. Then from [ ab]=0 and from (1) it follows that sinφ=0. Therefore the vectors a And b collinear.

The theorem is proven.

Theorem 2. Length (modulus) of the vector product [ ab] equals area S parallelogram constructed on vectors reduced to a common origin a And b.

Proof. As you know, the area of ​​a parallelogram is equal to the product of the adjacent sides of this parallelogram and the sine of the angle between them. Hence:

Then the vector product of these vectors has the form:

Expanding the determinant over the elements of the first row, we obtain the decomposition of the vector a×b by basis i, j, k, which is equivalent to formula (3).

Proof of Theorem 3. Let's create all possible pairs of basis vectors i, j, k and calculate their vector product. It should be taken into account that the basis vectors are mutually orthogonal, form a right-handed triple and have unit length (in other words, we can assume that i={1, 0, 0}, j={0, 1, 0}, k=(0, 0, 1)). Then we have:

From the last equality and relations (4), we obtain:

Let's create a 3x3 matrix, the first row of which is the basis vectors i, j, k, and the remaining lines are filled with vector elements a And b:

Thus, the result of the vector product of vectors a And b will be a vector:

.

Example 2. Find the vector product of vectors [ ab], where is the vector a represented by two points. Starting point of vector a: , end point of the vector a: , vector b looks like .

Solution: Move the first vector to the origin. To do this, subtract the coordinates of the starting point from the corresponding coordinates of the end point:

Let's calculate the determinant of this matrix by expanding it along the first row. The result of these calculations is the vector product of vectors a And b.

Definition. The vector product of vector a (multiplicand) and a non-collinear vector (multiplicand) is the third vector c (product), which is constructed as follows:

1) its module is numerically equal to the area of ​​the parallelogram in Fig. 155), built on vectors, i.e. it is equal to the direction perpendicular to the plane of the mentioned parallelogram;

3) in this case, the direction of the vector c is chosen (from two possible ones) so that the vectors c form a right-handed system (§ 110).

Designation: or

Addition to the definition. If the vectors are collinear, then considering the figure (conditionally) a parallelogram, it is natural to assign zero area. Therefore, the vector product of collinear vectors is considered equal to the null vector.

Since the null vector can be assigned any direction, this agreement does not contradict paragraphs 2 and 3 of the definition.

Remark 1. In the term “vector product” the first word indicates that the result of the action is a vector (as opposed to a scalar product; cf. § 104, remark 1).

Example 1. Find the vector product where are the main vectors of the right coordinate system (Fig. 156).

1. Since the lengths of the main vectors are equal to one scale unit, the area of ​​the parallelogram (square) is numerically equal to one. This means that the modulus of the vector product is equal to one.

2. Since the perpendicular to the plane is an axis, the desired vector product is a vector collinear to the vector k; and since both of them have modulus 1, the desired vector product is equal to either k or -k.

3. Of these two possible vectors, the first one must be chosen, since the vectors k form a right-handed system (and the vectors a left-handed one).

Example 2. Find the cross product

Solution. As in example 1, we conclude that the vector is equal to either k or -k. But now we need to choose -k, since the vectors form a right-handed system (and vectors form a left-handed one). So,

Example 3. Vectors have lengths equal to 80 and 50 cm, respectively, and form an angle of 30°. Taking the meter as the unit of length, find the length of the vector product a

Solution. The area of ​​a parallelogram built on vectors is equal to The length of the desired vector product is equal to

Example 4. Find the length of the vector product of the same vectors, taking centimeters as the unit of length.

Solution. Since the area of ​​a parallelogram constructed on vectors is equal, the length of the vector product is equal to 2000 cm, i.e.

From a comparison of examples 3 and 4 it is clear that the length of the vector depends not only on the lengths of the factors but also on the choice of the length unit.

Physical meaning of a vector product. Of the numerous physical quantities represented by the vector product, we will consider only the moment of force.

Let A be the point of application of force. The moment of force relative to point O is called a vector product. Since the modulus of this vector product is numerically equal to the area of ​​the parallelogram (Fig. 157), then the modulus of the moment is equal to the product of the base and the height, i.e., the force multiplied by the distance from point O to the straight line along which the force acts.

In mechanics, it is proven that for a rigid body to be in equilibrium, it is necessary that not only the sum of vectors representing the forces applied to the body be equal to zero, but also the sum of the moments of forces. In the case where all forces are parallel to one plane, the addition of vectors representing moments can be replaced by addition and subtraction of their magnitudes. But with arbitrary directions of forces, such a replacement is impossible. In accordance with this, the vector product is defined precisely as a vector, and not as a number.

Definition. The vector product of vector a and vector b is a vector denoted by the symbol [α, b] (or l x b), such that 1) the length of the vector [a, b] is equal to (p, where y is the angle between vectors a and b ( Fig. 31); 2) vector [a, b) is perpendicular to vectors a and b, i.e. perpendicular to the plane of these vectors; 3) the vector [a, b] is directed in such a way that from the end of this vector the shortest turn from a to b is seen to occur counterclockwise (Fig. 32). Rice. 32 Fig.31 In other words, vectors a, b and [a, b) form a right-hand triplet of vectors, i.e. located like the thumb, index and middle fingers of the right hand. If the vectors a and b are collinear, we will assume that [a, b] = 0. By definition, the length of the vector product is numerically equal to the area Sa of a parallelogram (Fig. 33), constructed on the multiplied vectors a and b as sides: 6.1 . Properties of a vector product 1. A vector product is equal to a zero vector if and only if at least one of the multiplied vectors is zero or when these vectors are collinear (if vectors a and b are collinear, then the angle between them is either 0 or 7r). Find the area of ​​the triangle (Fig. 36). It is clear that the area b"d of the triangle OAO is equal to half the area S of the parallelogram O AC B. Calculating the vector product (a, b| of the vectors a = OA and b = ob, we obtain Hence Remark: The vector product is not associative, i.e. the equality ( (a, b),c) = [a, |b,c)) is not true in the general case. For example, for a = ss j we have § 7. Mixed product of vectors Let us multiply the vectors a, b, and c. and 1> vector. As a result, we obtain the vector [a, 1>]. Let us multiply it scalarly by the vector c: (k b), c).The number ([a, b], e) is called the mixed product of the vectors a, b. and is denoted by the symbol (a, 1), e). vectors a, b and c are called coplanar in this case), then the mixed product ([a, b], c) = 0. This follows from the fact that the vector [a, b| is perpendicular to the plane in which the vectors a and 1 lie. ", and therefore to the vector c. / If the points O, A, B, C do not lie in the same plane (vectors a, b and c are non-coplanar), we will construct a parallelepiped on the edges OA, OB and OS (Fig. 38 a). By the definition of a vector product, we have (a,b) = So c, where So is the area of ​​the parallelogram OADB, and c is the unit vector perpendicular to the vectors a and b and such that the triple a, b, c is right-handed, i.e. vectors a, b and c are located respectively as the thumb, index and middle fingers of the right hand (Fig. 38 b). Multiplying both sides of the last equality on the right scalarly by the vector c, we obtain that the vector product of vectors given by coordinates. Mixed work. The number pc c is equal to the height h of the constructed parallelepiped, taken with the “+” sign if the angle between the vectors c and c is acute (triple a, b, c - right), and with the “-” sign if the angle is obtuse (triple a, b, c - left), so that Thus, the mixed product of vectors a, b and c is equal to the volume V of the parallelepiped built on these vectors as on edges, if the triple a, b, c is right, and -V, if the triple a , b, c - left. Based on the geometric meaning of the mixed product, we can conclude that by multiplying the same vectors a, b and c in any other order, we will always get either +7 or -K. Manufacturer's mark Fig. 38 reference will depend only on what kind of triple the multiplied vectors form - right or left. If the vectors a, b, c form a right-handed triple, then the triples b, c, a and c, a, b will also be right-handed. At the same time, all three triples b, a, c; a, c, b and c, b, a - left. Thus, (a,b, c) = (b,c, a) = (c,a,b) = -(b,a,c) = -(a,c,b) = -(c,b ,A). We emphasize again that the mixed product of vectors is equal to zero only if the multiplied vectors a, b, c are coplanar: (a, b, c are coplanar) 7.2. Mixed product in coordinates Let the vectors a, b, c be given by their coordinates in the basis i, j, k: a = (x\,y\,z]), b= (x2,y2>z2), c = (x3, uz, 23). Let us find an expression for their mixed product (a, b, c). We have a mixed product of vectors specified by their coordinates in the basis i, J, k, equal to the third-order determinant, the lines of which are composed respectively of the coordinates of the first, second and third of the multiplied vectors. The necessary and sufficient condition for the coplanarity of the vectors a y\, Z|), b = (хъ У2.22), с = (жз, з, 23) will be written in the following form У| z, ag2 y2 -2 =0. Uz Example. Check whether the vectors „ = (7,4,6), b = (2, 1,1), c = (19, II, 17) are coplanar. Calculate the height h of a parallelepiped built on vectors a = 31 + 2j - 5k, b = i- j + 4knc = i-3j + k, if a parallelogram built on vectors a and I is taken as the base. Answers

Obviously, in the case of a vector product, the order in which the vectors are taken matters, moreover,

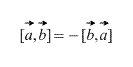
Also, directly from the definition it follows that for any scalar factor k (number) the following is true:

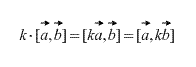
The cross product of collinear vectors is equal to the zero vector. Moreover, the cross product of two vectors is zero if and only if they are collinear. (In case one of them is a zero vector, it is necessary to remember that a zero vector is collinear to any vector by definition).

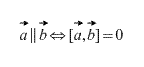
The vector product has distributive property, that is

Expressing the vector product through the coordinates of vectors.

Let two vectors be given

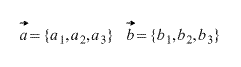
(how to find the coordinates of a vector from the coordinates of its beginning and end - see the article Dot product of vectors, item Alternative definition of the dot product, or calculating the dot product of two vectors specified by their coordinates.)

Why do you need a vector product?

There are many ways to use the cross product, for example, as written above, by calculating the cross product of two vectors you can find out whether they are collinear.

Or it can be used as a way to calculate the area of ​​a parallelogram constructed from these vectors. Based on the definition, the length of the resulting vector is the area of ​​the given parallelogram.

Online vector product calculator.

To find the scalar product of two vectors using this calculator, you need to enter the coordinates of the first vector in the first line in order, and the second in the second line. The coordinates of vectors can be calculated from the coordinates of their beginning and end (see article Dot product of vectors, item An alternative definition of dot product, or calculating the dot product of two vectors given by their coordinates.)

7.1. Definition of cross product

Three non-coplanar vectors a, b and c, taken in the indicated order, form a right-handed triplet if, from the end of the third vector c, the shortest turn from the first vector a to the second vector b is seen to be counterclockwise, and a left-handed triplet if clockwise (see Fig. . 16).

The vector product of vector a and vector b is called vector c, which:

1. Perpendicular to vectors a and b, i.e. c ^ a and c ^ b ;

2. Has a length numerically equal to the area of ​​a parallelogram constructed on vectors a andb as on the sides (see Fig. 17), i.e.

3. Vectors a, b and c form a right-handed triple.

The cross product is denoted a x b or [a,b]. The following relations between the unit vectors i directly follow from the definition of the vector product, j And k

(see Fig. 18):
i x j = k, j x k = i, k x i = j. Let us prove, for example, that

i xj =k. ^ 1) k ^ i, k

j ; 2) |k |=1, but | i x j

| = |i | And|J | sin(90°)=1;

3) vectors i, j and

form a right triple (see Fig. 16).

7.2. Properties of a cross product = -(1. When rearranging the factors, the vector product changes sign, i.e.).

and xb =(b xa) (see Fig. 19).

Vectors a xb and b xa are collinear, have the same modules (the area of ​​the parallelogram remains unchanged), but are oppositely directed (triples a, b, a xb and a, b, b x a of opposite orientation). That is axb b xa b 2. The vector product has a combining property with respect to the scalar factor, i.e. l ​​(a xb) = (l a) x b = a x (l b). b Let l >0. Vector l (a xb) is perpendicular to vectors a and b. Vector ( axb l axb a)x axb b xa b collinear. It is obvious that their directions coincide. They have the same length:

That's why axb(a xb)= axb a xb. It is proved in a similar way for axb<0.

3. Two non-zero vectors a and b are collinear if and only if their vector product is equal to the zero vector, i.e. a ||b<=>and xb =0.

In particular, i *i =j *j =k *k =0 .

4. The vector product has the distribution property:

(a+b) xc = a xc + b xs.

We will accept without proof.

7.3. Expressing the cross product in terms of coordinates

We will use the cross product table of vectors i, The following relations between the unit vectors i directly follow from the definition of the vector product, and k:

if the direction of the shortest path from the first vector to the second coincides with the direction of the arrow, then the product is equal to the third vector; if it does not coincide, the third vector is taken with a minus sign.

Let two vectors a =a x i +a y be given The following relations between the unit vectors i directly follow from the definition of the vector product,+a z And and b =b x i+b y The following relations between the unit vectors i directly follow from the definition of the vector product,+b z And. Let's find the vector product of these vectors by multiplying them as polynomials (according to the properties of the vector product):

The resulting formula can be written even more briefly:

since the right side of equality (7.1) corresponds to the expansion of the third-order determinant in terms of the elements of the first row. Equality (7.2) is easy to remember.

7.4. Some applications of cross product

Establishing collinearity of vectors

Finding the area of ​​a parallelogram and a triangle

According to the definition of the vector product of vectors A and b |a xb | =|a | * |b |sin g, i.e. S pairs = |a x b |. And, therefore, D S =1/2|a x b |.

Determination of the moment of force about a point

Let a force be applied at point A F =AB let it go ABOUT- some point in space (see Fig. 20).

It is known from physics that moment of force F relative to the point ABOUT called a vector M, which passes through the point ABOUT And:

1) perpendicular to the plane passing through the points O, A, B;

2) numerically equal to the product of force per arm

3) forms a right triple with vectors OA and A B.

Therefore, M = OA x F.

Finding linear rotation speed

Speed v point M of a rigid body rotating with angular velocity w around a fixed axis, is determined by Euler’s formula v =w xr, where r =OM, where O is some fixed point of the axis (see Fig. 21).