Predavanje iz matematike na temu "znak okomitosti dviju ravnina". Stereometrija Dokažite da su dvije ravnine okomite

Okomitost ravnina Definicija. Dvije se ravnine nazivaju okomitima ako je linearni kut na rubu diedralnog kuta između tih ravnina ravna crta.
Znak okomitost ravnina. Ako ravnina prolazi pravcem okomitim na drugu ravninu, tada su te ravnine okomite.
Dokaz. Neka a i ? - dvije ravnine koje se sijeku, S- linija njihovog sjecišta i A- ravno okomito na ravninu? i leži u avionua. A - točka sjecišta linijaa I S. U avionu? od točke I obnovit ćemo okomito, i neka bude ravna crta b. Ravno A okomito avion? , što znači da je okomita na bilo koju ravnu liniju u ovoj ravnini, odnosno na prave b I Sokomito . Kut između ravnih linija A I b - linearne ravnine a i ? a jednak je 90°, dakle Kako ravno A okomito na ravnu linijub(dokazano).Prema definiciji ravninea i ? okomito.

Teorem 1. Ako iz točke koja pripada jednoj od dviju okomitih ravnina povučemo okomita na drugu ravninu, onda ta okomica u cijelosti leži u prvoj ravnini.
Dokaz. Neka a i ? - okomite ravnine i sa - pravac njihovog sjecišta, A - točka a ležati ravno S. a ne izravno pripadajući a Neka okomito na ravninu? povučena iz točke A ne leži u ravnini , tada je točka C baza ova okomica leži u S. avion? a ne pripada liniji S. Iz točke A spustimo okomicu ABdirektnoPravac AB je okomitravnina (koristim teorem 2). Kroz pravac AB i točku C ? Hoćemo li nacrtati avion? (pravac i točka određuju ravninu i to samo jednu). To vidimo u avion a.

iz jedne točke A na pravac BC povučene su dvije okomice, što se ne može dogoditi, što znači pravac AC. poklapa se s ravnom linijom AB, a ravna linija AB, zauzvrat, potpuno leži u ravniniTeorem 2
Dokaz. Neka a Ako u jednoj od dviju okomitih ravnina povučemo okomicu na njihov pravac - okomite ravnine i sjecište, tada će ova okomica biti okomita na drugu ravninu. i ?- dvije okomite ravnine, linija njihova sjecišta i S i leži u avionuaA - A I S. ravno okomito na ravnu liniju . A - točka sjecišta linijaU avionu A Ib? iz točke A vratimo okomicu i neka bude ravna crta b. avionima a i ? a jednak je 90°, budući da ravninaa i ? okomito. Ravno A okomito na ravnu linijub(prema dokazanom) i izravni S po stanju. Dakle, ravno je A okomito na ravninu? (

Ovaj članak je posvećen okomitim ravninama. Definicije i oznake bit će dane zajedno s primjerima. Formulirati će se znak okomitosti ravnina i uvjet pod kojim je on zadovoljen. O rješenjima sličnih problema raspravljat ćemo na primjerima.

Yandex.RTB R-A-339285-1

Ako između pravaca koji se sijeku postoji kut, možemo govoriti o definiranju okomitih ravnina.

Definicija 1

Pod uvjetom da je kut između okomitih linija 90 stupnjeva, nazivaju se okomito.

Oznaka okomitosti obično se piše znakom “⊥”. Ako uvjet kaže da su ravnine α i β okomite, tada unos ima oblik α ⊥ β. Slika ispod prikazuje detalje.

Kada je u zaglavlju zadano da su ravnine α i β okomite, to znači da je α okomita na β i obrnuto. Takve se ravnine nazivaju međusobno okomitima. Na primjer, zid i strop u prostoriji su međusobno okomiti, jer kada se sijeku tvore pravi kut.

Okomitost ravnina - znak i uvjet okomitosti

U praksi se mogu susresti zadaci u kojima je potrebno odrediti okomitost zadanih ravnina. Prvo morate odrediti kut između njih. Ako je jednak 90 stupnjeva, tada se smatraju okomitima od definicije.

Za dokazivanje okomitosti dviju ravnina koristi se oznaka okomitosti dviju ravnina. Formulacija sadrži pojmove okomitog pravca i ravnine. Napišimo točnu definiciju kriterija okomitosti u obliku teorema.

Teorem 1

Ako jedna od dvije zadane ravnine siječe pravac okomit na drugu ravninu, tada su zadane ravnine okomite.

Dokaz je dostupan u udžbeniku geometrije za 10. - 11. razred, gdje je detaljan opis. Iz znaka slijedi da ako je ravnina okomita na presjek dviju zadanih ravnina, onda je okomita na svaku od tih ravnina.

Za dokaz postoji nužan i dovoljan uvjet. Razmotrimo ih za okomitost dviju zadanih ravnina, koja služi kao provjera njihove okomitosti, smještene u pravokutnom koordinatnom sustavu trodimenzionalnog prostora. Da bi dokaz bio valjan, potrebno je primijeniti definiciju vektora normale ravnine, kojom se dokazuje nužan i dovoljan uvjet okomitosti ravnina.

Teorem 2

Da bi okomitost ravnina koje se sijeku bila očita, potrebno je i dovoljno da se normalni vektori zadanih ravnina sijeku pod pravim kutom.

Dokaz

Neka je zadan pravokutni koordinatni sustav u trodimenzionalnom prostoru. Ako imamo n 1 → = (A 1, B 1, C 1) i n 2 → = (A 2, B 2, C 2), koji su normalni vektori zadanih ravnina α i β, tada je potrebna i dovoljna uvjet za okomitost vektora n 1 → i n 2 → poprimit će oblik

n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B 2 + C 1 · C 2 = 0

Odavde dobivamo da su n 1 → = (A 1, B 1, C 1) i n 2 → = (A 2, B 2, C 2) normalni vektori zadanih ravnina, a za stvarnost okomitosti α i β potrebno je i dovoljno, tako da skalarni umnožak vektora n 1 → i n 2 → bude jednak nuli, pa stoga ima oblik n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B 2 + C 1 · C 2 = 0 .

Jednakost je ispunjena.

Pogledajmo pobliže primjere.

Primjer 1

Odredite okomitost ravnina navedenih u pravokutnom koordinatnom sustavu O x y z trodimenzionalnog prostora određenog jednadžbama x - 3 y - 4 = 0 i x 2 3 + y - 2 + z 4 5 = 1?

Riješenje

Da biste pronašli odgovor na pitanje okomitosti, prvo trebate pronaći koordinate normalnih vektora zadanih ravnina, nakon čega možete provjeriti okomitost.

x - 3 y - 4 = 0 je opća jednadžba ravnine iz koje se odmah mogu transformirati koordinate normalnog vektora, jednake n 1 → = (1, - 3, 0).

Da bismo odredili koordinatu vektora normale ravnine x 2 3 + y - 2 + z 4 5 = 1, prijeđimo s jednadžbe ravnine u segmentima na opću.

Tada dobivamo:

x 2 3 + y - 2 + z 4 5 ⇔ 3 2 x - 1 2 y + 5 4 z - 1 = 0

Tada su n 2 → = 3 2, - 1 2, 5 4 koordinate vektora normale ravnine x 2 3 + y - 2 + z 4 5 = 1.

Prijeđimo na izračunavanje skalarnog produkta vektora n 1 → = (1, - 3, 0) i n 2 → = 3 2, - 1 2, 5 4.

Dobivamo da je n 1 → , n 2 → = 1 · 3 2 + (- 3) · - 1 2 + 0 · 5 4 = 3 .

Vidimo da nije jednak nuli, što znači da zadani vektori nisu okomiti. Slijedi da ravnine također nisu okomite. Uvjet nije ispunjen.

Odgovor: ravnine nisu okomite.

Primjer 2

Pravokutni koordinatni sustav O x y z ima četiri točke s koordinatama A - 15 4, - 7 8, 1, B 17 8, 5 16, 0, C 0, 0, 3 7, D - 1, 0, 0. Provjerite jesu li ravnine A B C i A B D okomite.

Riješenje

Prvo morate izračunati skalarni produkt vektora ovih ravnina. Ako je jednak nuli, samo u tom slučaju možemo smatrati da su okomiti. Nađemo koordinate normalnih vektora n 1 → i n 2 → ravnina A B C i A B D.

Iz zadanih koordinata točaka izračunamo koordinate vektora A B → , A C → , A D → . Dobivamo to:

A B → = 47 8, 19 16, - 1, A C → = 15 4, 7 8, - 4 7, A D → = 11 4, 7 8, - 1.

Vektor normale ravnine A B C je vektorski umnožak vektora A B → i A C →, a za A B D vektorski umnožak A B → i A D →. Odavde to dobivamo

n 1 → = A B → × A C → = i → j → k → 47 8 19 16 - 1 15 4 7 8 - 4 7 = 11 56 i → - 11 28 j → + 11 16 k → ⇔ n 1 → = 11 56 , - 11 28 , 11 16 n 2 → = A B → × A D → = i → j → k → 47 8 19 16 - 1 11 4 7 8 - 1 = - 5 16 i → + 25 8 j → + 15 8 k → ⇔ n 2 → = - 5 16 , 25 8 , 15 8

Počnimo s pronalaženjem skalarnog produkta n 1 → = 11 56, - ​​​​11 28, 11 16 i n 2 → = - 5 16, 25 8, 15 8.

Dobivamo: n 1 → , n 2 → = 11 56 · - 5 16 + - 11 28 · 25 8 + 11 16 · 15 8 = 0 .

Ako je jednak nuli, onda su vektori ravnina A B C i A B D okomiti, tada su i same ravnine okomite.

Odgovor: ravnine su okomite.

Moglo se drugačije pristupiti rješenju i koristiti jednadžbe ravnina A B C i A B D. Nakon pronalaženja koordinata normalnih vektora ovih ravnina, moglo bi se provjeriti je li zadovoljen uvjet okomitosti normalnih vektora ravnina.

Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter

Ova lekcija pomoći će onima koji žele razumjeti temu "Znak okomitosti dviju ravnina." Na početku ćemo ponoviti definiciju diedarskog i pravocrtnog kuta. Zatim ćemo razmotriti koje se ravnine nazivaju okomitima, te dokazati znak okomitosti dviju ravnina.

Tema: Okomitost pravca i ravnine

Lekcija: Znak okomitosti dviju ravnina

Definicija. Diedarski kut je lik kojeg tvore dvije poluravnine koje ne pripadaju istoj ravnini i njihov zajednički pravac a (a je brid).

Riža. 1

Promotrimo dvije poluravnine α i β (slika 1). Zajednička im je granica l. Taj se lik naziva diedralni kut. Dvije ravnine koje se sijeku tvore četiri diedra sa zajedničkim bridom.

Diedralni kut se mjeri svojim linearnim kutom. Odaberemo proizvoljnu točku na zajedničkom bridu l diedarskog kuta. U poluravninama α i β iz ove točke povučemo okomice a i b na pravac l i dobijemo linearni kut dvostranog kuta.

Pravci a i b tvore četiri kuta jednaka φ, 180° - φ, φ, 180° - φ. Podsjetimo se da je kut između ravnih linija najmanji od ovih kutova.

Definicija. Kut između ravnina je najmanji od diedarskih kutova koje čine te ravnine. φ je kut između ravnina α i β, ako

Definicija. Dvije ravnine koje se sijeku nazivaju se okomitima (međusobno okomitima) ako je kut između njih 90°.

Riža. 2

Na bridu l odabrana je proizvoljna točka M (slika 2). Povucimo dva okomita pravca MA = a i MB = b na brid l u ravnini α, odnosno u ravnini β. Dobili smo kut AMB. Kut AMB je linearni kut diedralnog kuta. Ako je kut AMB 90°, tada se ravnine α i β nazivaju okomitima.

Pravac b je konstrukcijski okomit na pravac l. Pravac b je okomit na pravac a jer je kut između ravnina α i β 90°. Utvrdimo da je pravac b okomit na dva pravca a i l koji se sijeku iz ravnine α. To znači da je pravac b okomit na ravninu α.

Slično možemo dokazati da je pravac a okomit na ravninu β. Pravac a je konstrukcijski okomit na pravac l. Pravac a je okomit na pravac b jer je kut između ravnina α i β 90°. Nalazimo da je pravac a okomit na dva pravca b i l koji se sijeku iz ravnine β. To znači da je pravac a okomit na ravninu β.

Ako jedna od dviju ravnina prolazi pravcem okomitim na drugu ravninu, tada su te ravnine okomite.

Dokazati:

Riža. 3

Dokaz:

Neka se ravnine α i β sijeku duž pravca AC (slika 3). Da bismo dokazali da su ravnine međusobno okomite, potrebno je konstruirati linearni kut između njih i pokazati da je taj kut 90°.

Pravac AB okomit je na ravninu β, a time i na pravac AC koji leži u ravnini β.

Povucimo pravac AD okomit na pravac AC u ravnini β. Tada je BAD linearni kut diedralnog kuta.

Pravac AB okomit je na ravninu β, a time i na pravac AD koji leži u ravnini β. To znači da je linearni kut BAD 90°. To znači da su ravnine α i β okomite, što je i trebalo dokazati.

Ravnina okomita na pravac po kojem se sijeku dvije zadane ravnine okomita je na svaku od tih ravnina (slika 4).

Dokazati:

Riža. 4

Dokaz:

Pravac l okomit je na ravninu γ, a ravnina α prolazi kroz pravac l. To znači da su prema okomitosti ravnina ravnine α i γ okomite.

Pravac l okomit je na ravninu γ, a ravnina β prolazi kroz pravac l. To znači da su na temelju okomitosti ravnina ravnine β i γ okomite.

Razmatra se odnos okomitosti ravnina - jedan od najvažnijih i najkorištenijih u geometriji prostora i njezinim primjenama.

Iz sve raznolikosti međusobnih dogovora

dvije ravnine, a posebnu pozornost i proučavanje zaslužuje ona u kojoj su ravnine okomite jedna na drugu (npr. ravnine susjednih zidova prostorije,

ograda i zemljište, vrata i pod, itd. (Sl. 417, a-c).

Gornji primjeri omogućuju nam da vidimo jedno od glavnih svojstava odnosa koji ćemo proučavati - simetriju položaja svake ravnine u odnosu na drugu. Simetrija je osigurana činjenicom da ravnine izgledaju kao da su "satkane" od okomica. Pokušajmo razjasniti ova zapažanja.

Neka nam je ravnina α i pravac c na njoj (slika 418, a). Povucimo kroz svaku točku pravca c prave okomite na ravninu α. Sve ove linije su paralelne jedna s drugom (zašto?) i, na temelju zadatka 1 § 8, tvore određenu ravninu β (slika 418, b). Prirodno je ravninu nazvati β okomito ravnina α.

S druge strane, sve ravne linije koje leže u ravnini α i okomite na ravne linije tvore ravninu α i okomite su na ravninu β (slika 418, c). Doista, ako je a proizvoljan pravac, tada on siječe pravac c u nekoj točki M. Točkom M u ravnini β prolazi pravac b okomit na α, dakle b a . Dakle, a c, a b, dakle a β. Dakle, ravnina α okomita je na ravninu β, a pravac je linija njihova sjecišta.

Dvije ravnine se nazivaju okomitima ako je svaka od njih sastavljena od ravnina koje su okomite na drugu ravninu i prolaze kroz sjecišta tih ravnina.

Okomitost ravnina α i β označena je poznatim znakom: α β.

Jednu ilustraciju ove definicije možemo zamisliti ako uzmemo u obzir fragment sobe u seoskoj kući (sl. 419). U njemu su pod i zid izrađeni od dasaka okomito na zid, odnosno pod. Stoga su okomiti. Na praksi

to znači da je pod vodoravan, a zid okomit.

Gornju definiciju teško je koristiti pri stvarnoj provjeri okomitosti ravnina. Ali ako pažljivo analiziramo obrazloženje koje je dovelo do ove definicije, vidimo da je okomitost ravnina α i β osigurana prisutnošću u ravnini β ravne crte b okomite na ravninu α (Sl. 418, c) . Došli smo do kriterija okomitosti dviju ravnina koji se najčešće koristi u praksi.

406 Okomitost pravaca i ravnine

Teorem 1 (test okomitosti ravnina).

Ako jedna od dvije ravnine prolazi pravcem okomitim na drugu ravninu, tada su te ravnine okomite.

 Neka ravnina β prolazi kroz pravac b okomit na ravninu α i sjecišna je linija ravnina α i β (slika 420, a). Svi pravci ravnine β, paralelni s pravcem b i sijeku pravac c, zajedno s pravcem b čine ravninu β. Prema teoremu o dva paralelna pravca, od kojih je jedan okomit na ravninu (teorem 1, § 19), svi su oni zajedno s pravcem b okomiti na ravninu α. To jest, ravnina β sastoji se od ravnih linija koje prolaze kroz liniju sjecišta ravnina α i β i okomite na ravninu α (slika 420, b).

Sada u ravnini α kroz točku A sjecišta linija b i nacrtamo liniju okomitu na liniju c (slika 420, c). Pravac je okomit na ravninu β, na temelju okomitosti pravca i ravnine (a c, prema konstrukciji, i b, jer je b α). Ponavljajući prethodne argumente, nalazimo da se ravnina α sastoji od pravaca okomitih na ravninu β, koji prolaze kroz liniju presjeka ravnina. Prema definiciji ravnine α i β su okomite.■

Ova značajka omogućuje uspostavljanje okomitosti ravnina ili njezino osiguranje.

Primjer 1. Pričvrstite štit na stup tako da bude postavljen okomito.

 Ako stup stoji okomito, tada je dovoljno nasumično pričvrstiti štit na stup i učvrstiti ga (slika 421, a). Prema značajci koja je gore razmotrena, ravnina štita bit će okomita na površinu zemlje. U ovom slučaju problem ima beskonačan broj rješenja.

Ako stup stoji koso prema tlu, tada je dovoljno na stup pričvrstiti okomitu šinu (sl. 421, b), a zatim pričvrstiti štit i na šinu i na stup. U ovom slučaju, položaj štita bit će sasvim određen, budući da stup i šina definiraju jednu ravninu.■

U prethodnom primjeru, “tehnički” zadatak je sveden na matematički problem o crtanju ravnine okomite na drugu ravninu kroz zadanu ravnu crtu.

Primjer 2. Iz vrha A kvadrata ABCD povučena je dužina AK okomito na njegovu ravninu, AB = AK = a.

1) Odrediti međusobni položaj ravnina AKC i ABD,

AKD i ABK.

2) Konstruirajte ravninu koja prolazi pravcem BD okomito na ravninu ABC.

3) Kroz sredinu F segmenta KC nacrtaj ravninu okomitu na ravninu KAC.

4) Pronađite površinu trokuta BDF.

 Konstruirajmo crtež koji odgovara uvjetima primjera (slika 422).

1) Ravnine AKC i ABD su okomite, prema svojstvu okomitosti ravnina (teorem 1): AK ABD, prema uvjetu. Ravnine AKD i ABK također su okomite

su polarne, temeljene na okomitosti ravnina (teorem 1). Doista, pravac AB kroz koji prolazi ravnina ABK okomit je na ravninu AKD, prema znaku okomitosti pravca i ravnine (teorem 1 § 18): AB AD kao susjedne stranice kvadrata;

AK ABD.

2) Na temelju okomitosti ravnina, za željenu konstrukciju dovoljno je povući ravnu liniju BD kroz neke točke

408 Okomitost pravaca i ravnina

pravac okomit na ravninu ABC. A da biste to učinili, dovoljno je nacrtati liniju paralelnu s ravnom linijom AK kroz ovu točku.

Doista, prema uvjetu, pravac AK je okomit na ravninu ABC i stoga, prema teoremu o dvije paralelne prave,

Teorem 2 (o okomici na presjek okomitih ravnina).

Ako su dvije ravnine okomite, onda je pravac koji pripada jednoj ravnini i okomit na sjecište tih ravnina okomit na drugu ravninu.

 Neka okomite ravnine

α i β sijeku se duž pravca c, a pravac b u ravnini β okomit je na pravac c i siječe ga u točki B (sl. 425). Po definiciji

koja dijeli okomitost ravnina, u ravnini β kroz točku B prolazi pravac

b 1, okomito na ravninu α. Jasno je da je okomita na ravnu liniju. Ali što-

Ako izrežete točku na ravnoj liniji u ravnini, možete povući samo jednu ravnu crtu okomitu na zadanu ravnu crtu. Zato

pravci b i b 1 se podudaraju. To znači da je pravac jedne ravnine, okomit na sjecište dviju okomitih ravnina, okomit na drugu ravninu. ■

Primijenimo razmatrani teorem na obrazloženje drugog znaka okomitosti ravnina, što je važno s gledišta kasnijeg proučavanja relativnog položaja dviju ravnina.

Neka su ravnine α i β okomite, pravac c je linija njihova sjecišta. Kroz proizvoljnu točku A povučemo ravnu crtu c

u ravninama α i β, pravci a i b, okomiti na pravce c (slika 426). Prema teoriji

Me 2, pravci a i b okomiti su na ravnine β odnosno α, pa su međusobno okomiti: a b . Ravno

definirani a i b definiraju određenu ravninu γ. Pravac presjeka s ravninama α i β

okomito na ravninu γ, na temelju okomitosti pravca i ravnine (teorem 1 § 18): c a, c b, a γ, b γ. Ako uzmemo u obzir proizvoljnost izbora točke A na pravoj liniji c i činjenicu da jedina ravnina okomita na nju prolazi kroz točku A prave, tada možemo izvući sljedeći zaključak.

Teorem 3 (o ravnini okomitoj na presjek okomitih ravnina).

Ravnina okomita na presjek dviju okomitih ravnina siječe te ravnine po okomitim ravnim crtama.

Time je utvrđeno još jedno svojstvo okomitih ravnina. Ovo svojstvo je karakteristično, odnosno ako vrijedi za neke dvije ravnine, tada su ravnine okomite jedna na drugu. Imamo još jedan znak okomitosti ravnina.

Teorem 4 (drugi kriterij za okomitost ravnina).

Ako su izravna sjecišta dviju ravnina s trećom ravninom okomitom na crtu njihova sjecišta okomita, onda su i te ravnine okomite.

 Neka se ravnine α i β sijeku duž pravca s, a ravnina γ, okomita na pravac s, siječe ravnine α i β odgovarajuće.

odnosno duž ravnih linija a i b (slika 427). Prema uvjetu, a b . Kako je γc, onda c. I zato je pravac okomit na ravninu β, prema predznaku okomitosti pravca i ravnine (teorem 1 § 18). To je to-

da, slijedi da su ravnine α i β okomite, prema znaku okomitosti ravnina (teorem 1).■

Također su vrijedni pažnje teoremi o vezama između okomitosti dviju ravnina treće ravnine i njihovog međusobnog položaja.

Teorem 5 (o presjecištu dviju ravnina okomitih na treću ravninu).

Ako se dvije ravnine okomite na treću ravninu sijeku, tada je linija njihova sjecišta okomita na tu ravninu.

 Neka se ravnine α i β, okomite na ravninu γ, sijeku duž pravca (a || γ), a A je točka presjeka pravca s

Razmotrimo teorem koji opisuje odnos između paralelizma i okomitosti ravnina. Već smo imali odgovarajući rezultat za prave i ravnine.

Teorem 6 (o paralelnim ravninama okomitim na treću ravninu).

Ako je jedna od dvije paralelne ravnine okomita na treću, onda je i druga ravnina okomita na nju.

 Neka su ravnine α i β paralelne, a ravnina γ okomita na ravninu α. Budući da je ravnina γ

siječe ravninu α, onda mora sijeći i ravninu β paralelnu s njom. Uzmimo pro-

proizvoljnu ravninu m okomitu na ravninu γ i kroz nju, kao i kroz proizvoljnu točku ravnine β, povući ravninu δ (slika 429).

Ravnine δ i β sijeku se duž pravca n, a budući da je α║ β, onda je ║ n (Teorem 2 §18). Iz teorema 1 slijedi da je γ, pa će stoga i ravnina β koja prolazi kroz pravac također biti okomita na ravninu γ. ■

Dokazani teorem daje još jedan znak okomitosti ravnina.

Kroz zadanu točku pomoću znaka okomitosti ravnina možete povući ravninu okomitu na zadanu točku (teorem 1). Dovoljno je kroz tu točku povući pravac okomit na zadanu ravninu (vidi zadatak 1 § 19). Zatim nacrtajte ravninu kroz konstruiranu ravnu liniju. Ona će biti okomita na zadanu ravninu prema navedenom kriteriju. Jasno je da se može nacrtati beskonačno mnogo takvih ravnina.

Smisleniji je problem konstruiranja ravnine okomite na zadanu, pod uvjetom da prolazi kroz zadani pravac. Jasno je da ako je dani pravac okomit na danu ravninu, tada se može konstruirati beskonačan broj takvih ravnina. Preostaje razmotriti slučaj kada zadani pravac nije okomit na zadanu ravninu. Mogućnost takve konstrukcije opravdana je na razini fizičkih modela ravnina i ravnina u primjeru 1.

Zadatak 1. Dokažite da se kroz proizvoljan pravac koji nije okomit na ravninu može povući ravnina okomita na zadanu ravninu.

 Neka su zadane ravnina α i pravac l, l B\ a. Uzmimo proizvoljnu točku M na ravnoj crti i povucimo kroz nju ravnu liniju, okomitu na ravninu α (slika 430, a). Kako prema uvjetu l nije okomit na α, tada se pravci l koje sijeku. Kroz te ravne linije moguće je povući ravninu β (slika 430, b), koja će, prema testu okomitosti ravnina (teorem 1), biti okomita na ravninu α. ■

Primjer 3. Kroz vrh A pravilne piramide SABC s osnovicom ABC povuci pravac okomit na ravninu bočne plohe SBC.

 Za rješavanje ovog problema koristimo teorem o okomici na presjek okomitih ravnina

(Teorem 2). Neka je K polovište brida BC (sl. 431). Ravnine AKS i BCS su okomite, prema znaku okomitosti ravnina (teorem 1). Doista, BC SK i BC AK su poput središnjica povučenih na osnovice u jednakokračnim trokutima. Dakle, prema kriteriju okomitosti pravca i ravnine (teorem 1 §18), pravac BC okomit je na ravninu AKS. Ravnina BCS prolazi pravcem okomitim na ravninu AKS.

Izgradnja. Povucimo iz točke A pravac AL u ravnini AKS, okomit na pravac KS - presjecište ravnina AKS i BCS (sl. 432). Prema teoremu o okomici na presjek okomitih ravnina (teorem 2), pravac AL je okomit na ravninu BCS. ■

2. Na sl. 434 je ispravno prikazan- nova četverokutna piramida

SABCD, točke P, M, N - sredina -

Imamo bridove AB, BC, BS, O - središte baze ABCD. Koji su od parova ravni- kosti su okomite:

1) ACS i BDS 2) MOS i POS;

3) COS i MNP; 4) MNP i SOB;

5) CND i ABS?

3) PAC i PBC; 4) PAC i PAB?

4. Dvije ravnine su okomite. Je li moguće kroz proizvoljnu točku jednog od trebaju nacrtati ravnu liniju u ovoj ravnini, drugoj ravnini?

5. Nemoguće je nacrtati ravnu liniju u α ravnini, ali ne i u β ravnini. Mogu li ovi avioni biti mi?

6. Kroz određenu točku na ravnini α prolazi pravac u toj ravnini i okomit je na ravninu, tako da su ravnine α i β okomite?

Dio ograde je pričvršćen za okomiti stup, može li se tvrditi da je ravnina ograde okomita?

Kako pričvrstiti štit okomito na tračnicu paralelnu s površinom zemlje?

Zašto su površine vrata, bez obzira jesu li zatvorena ili otvorena, okomite na pod?

Zašto visak čvrsto prianja uz okomiti zid, ali ne nužno i uz nagnuti zid?

Je li moguće pričvrstiti štit na nagnuti stup tako da bude okomit na površinu zemlje?

Kako praktično odrediti je li ravnina okomita

zidovi ravni pod? okomit okomit okomit okomit- ravno, ležeći - β. Istina 7. . Moguće 8.9.10.11.12.

Grafičke vježbe

1. Na sl. 436 prikazuje kocku ABCDA 1 B 1 C 1 D 1 .

1) Navedite ravnine okomite na ravninu VDD 1.

2) Kako su avioni i

A1 B1 KABINA 1 C 1

421. Isječak OS povučen je iz središta O kvadrata ABCD okomito na njegovu ravninu.

1°) Odredite međusobni položaj ravnina ACS

i ABC.

2°) Odrediti međusobni položaj ravnina ACS

i BDS.

3) Konstruirajte ravninu koja prolazi pravcem OS okomito na ravninu ABS.

4) Konstruirajte ravninu okomitu na ravninu ABC koja prolazi središtima stranica AD i CD.

422. Iz sjecišta O dijagonala romba ABCD povučena je dužina OS okomita na ravninu romba AB = DB =

1°) Odredi relativni položaj SDB i

ABC, SDB i ACS.

2°) Konstruirajte ravninu koja prolazi pravcem BC okomito na ravninu ABD.

3) Kroz sredinu segmenta F nacrtaj ravninu okomitu na ravninu ABC.

4) Pronađite površinu trokuta BDF.

423. Dana je kocka ABCDA1 B1 C1 D1.

1°) Odredi međusobni položaj ravnina AB 1 C 1

i CDD1.

2°) Odredi međusobni položaj ravnina AB 1 C 1

i CD1 A1.

3°) Konstruirajte ravninu koja prolazi točkom A okomito na ravninu BB 1 D 1.

4) Konstruirajte presjek kocke ravninom koja prolazi središtima bridova A 1 D 1 i B 1 C 1 okomito na ravninu ABC. 5) Odredite međusobni položaj ravnine AA 1 B i ravnine koja prolazi sredinom rebara A 1 B 1, C 1 D 1, CD.

6) Pronađite površinu poprečnog presjeka kocke ravninom koja prolazi kroz rub BB 1 i sredinu ruba A 1 D 1 (BB ​​​​1 = a).

7) Konstruirajte točku simetričnu točki A u odnosu na ravninu A 1 B 1 C.

424. U pravilnom tetraedru ABCD brida 2 cm točka M je sredina DB, a točka N sredina AC.

1°) Dokažite da je pravac DB okomit na ravninu

2°) Dokažite da je ravnina BDM okomita na ravninu AMC.

3) Kroz točku O sjecišta središnjica trokuta ADC povucite ravnu crtu okomitu na ravninu AMC.

4) Pronađite duljinu ovog segmenta unutar tetraedra. 5) U kojem omjeru AMC ravnina dijeli ovaj segment?

425. Dva jednakostranična trokuta ABC i ADC leže u okomitim ravninama.

1°) Odredi duljinu odsječka BD ako je AC = 1 cm.

2) Dokažite da je ravnina BKD (K leži na pravcu AC) okomita na ravninu svakog od trokuta ako i samo ako je K polovište stranice AC.

426. Pravokutnik ABCD čije su stranice 3 cm i 4 cm savijen je duž dijagonale AC tako da su trokuti ABC i ADC bili u okomitim ravninama. Odredi udaljenost između točaka B i D nakon savijanja pravokutnika ABCD.

427. Kroz tu točku povuci ravninu okomitu na svaku od dviju zadanih ravnina.

428°. Dokažite da su ravnine susjednih ploha kocke okomite.

429. Ravnine α i β međusobno su okomite. Iz točke A ravnine α povučena je pravac AB okomita na ravninu β. Dokažite da pravac AB leži u ravnini α.

430. Dokažite da ako su ravnina i pravac koji ne leži u toj ravnini okomiti na istu ravninu, onda su međusobno paralelni.

431. Kroz točke A i B koje leže na presjecištu ravnina α i β koje su okomite jedna na drugu, povučene su okomite prave: AA 1 u α, BB 1 u β. Točka X leži na pravcu AA 1, a točka Y na BB 1. Dokažite da je pravac VB 1 okomit na pravac VH, a pravac AA 1 okomit na pravac AY.

432*. Kroz sredinu svake stranice trokuta povučena je ravnina okomita na ovu stranicu. Dokažite da se sve tri nacrtane ravnine sijeku po jednoj ravnoj crti okomitoj na ravninu trokuta.

Vježbe za ponavljanje

433. U jednakostraničnom trokutu sa stranicom b odrediti: 1) visinu; 2) polumjeri upisane i opisane kružnice.

434. Iz jedne točke na zadani pravac povučeni su okomit i dva kosa pravca. Odredite duljinu okomice ako su nagnute okomice 41 cm i 50 cm, a njihove su projekcije na taj pravac u omjeru 3:10.

435. Odredite katete pravokutnog trokuta ako bis- sektrisa pravog kuta dijeli hipotenuzu na odsječke od 15 cm i

Osnovna definicija

Dva aviona su tzv

su okomiti , ako je svaki od njih oblikovan ravnim linijama- mi, okomito- mi druge ravnine i prolazi kroz sjecišne točke tih ravnina.

Pojam okomitih ravnina

Kada se dvije ravnine sijeku, dobivamo $4$ diedralnih kutova. Dva su kuta jednaka $\varphi $, a druga dva su jednaka $(180)^0-\varphi $.

Definicija 1

Kut između ravnina je najmanji od diedarskih kutova koje čine te ravnine.

Definicija 2

Dvije ravnine koje se sijeku nazivaju se okomitima ako je kut između tih ravnina $90^\circ$ (slika 1).

Slika 1. Okomite ravnine

Znak okomitosti dviju ravnina

Teorem 1

Ako je ravnina ravnine okomita na drugu ravninu, onda su te ravnine okomite jedna na drugu.

Dokaz.

Neka su nam zadane ravnine $\alpha $ i $\beta $ koje se sijeku duž pravca $AC$. Neka je pravac $AB$ koji leži u $\alpha $ ravnini okomit na $\beta $ ravninu (slika 2).

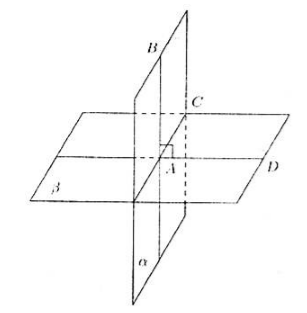
Slika 2.

Budući da je pravac $AB$ okomit na ravninu $\beta$, okomit je i na pravac $AC$. Nacrtajmo dodatno pravac $AD$ u $\beta $ ravnini, okomit na pravac $AC$.

Nalazimo da je kut $BAD$ linearni kut diedralnog kuta, jednak $90^\circ$. Odnosno, prema definiciji 1, kut između ravnina je $90^\circ$, što znači da su te ravnine okomite.

Teorem je dokazan.

Iz ovog teorema slijedi sljedeći teorem.

Teorem 2

Ako je ravnina okomita na pravac po kojem se sijeku druge dvije ravnine, onda je okomita i na te ravnine.

Dokaz.

Neka su nam zadane dvije ravnine $\alpha $ i $\beta $ koje se sijeku duž pravca $c$. Ravnina $\gamma $ je okomita na ravnu liniju $c$ (Sl. 3)

Slika 3.

Budući da pravac $c$ pripada ravnini $\alpha $, a ravnina $\gamma $ je okomita na pravac $c$, tada su prema teoremu 1 ravnine $\alpha $ i $\gamma $ okomite.

Budući da pravac $c$ pripada ravnini $\beta $ i da je ravnina $\gamma $ okomita na pravac $c$, tada su prema teoremu 1 ravnine $\beta $ i $\gamma $ okomite.

Teorem je dokazan.

Za svaki od ovih teorema vrijede i obratne tvrdnje.

Primjeri problema

Primjer 1

Neka nam je dan pravokutni paralelopiped $ABCDA_1B_1C_1D_1$. Nađi sve parove okomitih ravnina (slika 5).

Slika 4.

Riješenje.

Prema definiciji pravokutnog paralelopipeda i okomitih ravnina, vidimo sljedećih osam parova ravnina okomitih jedna na drugu: $(ABB_1)$ i $(ADD_1)$, $(ABB_1)$ i $(A_1B_1C_1)$, $( ABB_1)$ i $(BCC_1) $, $(ABB_1)$ i $(ABC)$, $(DCC_1)$ i $(ADD_1)$, $(DCC_1)$ i $(A_1B_1C_1)$, $(DCC_1) $ i $(BCC_1)$, $(DCC_1)$ i $(ABC)$.

Primjer 2

Neka su nam zadane dvije međusobno okomite ravnine. Iz točke jedne ravnine povučena je okomica na drugu ravninu. Dokažite da taj pravac leži u zadanoj ravnini.

Dokaz.

Neka su nam zadane okomite ravnine $\alpha $ i $\beta $ koje se sijeku duž pravca $c$. Iz točke $A$ ravnine $\beta $ povučena je okomica $AC$ na ravninu $\alpha $. Pretpostavimo da $AC$ ne leži u $\beta$ ravnini (slika 6).

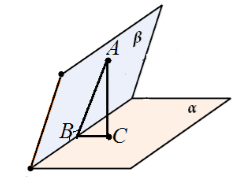
Slika 5.

Promotrimo trokut $ABC$. Pravokutan je s pravim kutom $ACB$. Prema tome, $\kut ABC\ne (90)^0$.

Ali s druge strane, $\kut ABC$ je linearni kut diedralnog kuta kojeg čine te ravnine. To jest, diedralni kut koji čine te ravnine nije jednak 90 stupnjeva. Nalazimo da kut između ravnina nije jednak $90^\circ$. Kontradikcija. Dakle, $AC$ leži u $\beta$ ravnini.