Piramida. Formule in lastnosti piramide. Kako izračunati površino piramide: osnova, stran in skupno

Ploščina stranske ploskve poljubne piramide je enaka vsoti površin njenih stranskih ploskev. Smiselno je podati posebno formulo za izražanje tega območja v primeru pravilne piramide. Torej nam je podana pravilna piramida, na osnovi katere leži pravilen n-kotnik s stranico, enako a. Naj bo h višina stranske ploskve, imenovane tudi apotema piramide. Ploščina ene stranske ploskve je enaka 1/2ah, celotna stranska ploskev piramide pa ima ploščino n/2ha. Ker je na obod osnove piramide, lahko zapišemo najdeno formulo v obliki:

Bočna površina pravilne piramide je enak zmnožku njenega apotema in polovice oboda osnove.

Glede skupna površina, potem preprosto dodamo površino osnove stranski.

Včrtana in opisana krogla in krogla. Upoštevati je treba, da središče krogle, včrtane v piramido, leži na presečišču simetralnih ravnin notranjih diedrskih kotov piramide. Središče krogle, opisane v bližini piramide, leži na presečišču ravnin, ki potekajo skozi središča robov piramide in so pravokotne nanje.

Prisekana piramida.Če piramido prereže ravnina, ki je vzporedna z njeno osnovo, potem se del med sečno ravnino in osnovo imenuje prisekana piramida. Na sliki je prikazana piramida, če zavržemo njen del, ki leži nad sečno ravnino, dobimo prisekano piramido. Jasno je, da je majhna zavržena piramida homotetična veliki piramidi s središčem homotetije na vrhu. Koeficient podobnosti je enak razmerju višin: k=h 2 /h 1 ali stranskih robov ali drugih ustreznih linearnih dimenzij obeh piramid. Vemo, da so površine podobnih likov povezane kot kvadrati linearnih dimenzij; tako sta ploščini baz obeh piramid (tj. ploščina baz prisekane piramide) povezani kot

Tukaj je S 1 območje spodnje baze, S 2 pa območje zgornje baze prisekane piramide. Stranske površine piramid so v enakem razmerju. Podobno pravilo velja za količine.

Prostornine podobnih teles so povezani kot kocke svojih linearnih dimenzij; na primer, prostornine piramid so povezane kot zmnožek njihovih višin in površine baz, iz česar takoj dobimo naše pravilo. Je povsem splošne narave in neposredno izhaja iz dejstva, da ima prostornina vedno razsežnost tretje dolžinske potence. S tem pravilom izpeljemo formulo, ki izraža prostornino prisekane piramide skozi višino in površino baz.

Naj bo podana prisekana piramida z višino h in osnovnima ploščinama S 1 in S 2 . Če si predstavljamo, da jo razširimo na polno piramido, potem koeficient podobnosti med polno piramido in malo piramido zlahka najdemo kot koren razmerja S 2 /S 1 . Višina prisekane piramide je izražena kot h = h 1 - h 2 = h 1 (1 - k). Zdaj imamo za prostornino prisekane piramide (V 1 in V 2 označujeta prostornino polne in male piramide)

formula za prostornino prisekane piramide

Izpeljimo formulo za ploščino S stranske ploskve pravilne prisekane piramide skozi oboda P 1 in P 2 baz in dolžino apoteme a. Razmišljamo popolnoma enako kot pri izpeljavi formule za prostornino. Piramido dopolnimo z zgornjim delom, imamo P 2 = kP 1, S 2 = k 2 S 1, kjer je k koeficient podobnosti, P 1 in P 2 sta oboda baz, S 1 in S 2 so površine stranskih ploskev celotne nastale piramide in njenega zgornjega dela v skladu s tem. Za stransko površino najdemo (a 1 in a 2 sta apotema piramid, a = a 1 - a 2 = a 1 (1-k))

formula za stransko površino pravilne prisekane piramide

• Problem 1. Poiščite celotno površino piramide
• Problem 2. Poiščite stransko površino pravilne trikotne piramide

Problem 1. Poiščite skupno površino pravilne piramide

rešitev.

Na dnu pravilne trikotne piramide leži enakostranični trikotnik.
Zato bomo za rešitev problema uporabili lastnosti pravilnega trikotnika:

Poznamo višino trikotnika, od koder lahko poiščemo njegovo ploščino.
h = √3/2a
a = h / (√3/2)
a = 3 / (√3/2)
a = 6 / √3

Od koder bo površina baze enaka:
S = √3/4 a 2
S = √3/4 (6 / √3) 2
S = 3√3

Da bi našli površino stranske ploskve, izračunamo višino KM. Glede na nalogo je kot OKM 45 stopinj.
Tako:
OK / MK = cos 45
Uporabimo tabelo vrednosti trigonometričnih funkcij in nadomestimo znane vrednosti.

OK / MK = √2/2

Upoštevajmo, da je OK enak polmeru včrtanega kroga. Potem
OK = √3/6a
OK = √3/6 * 6/√3 = 1

Potem
OK / MK = √2/2
1/MK = √2/2
MK = 2/√2

Površina stranske ploskve je nato enaka polovici produkta višine in osnove trikotnika.
Sstran = 1/2 (6 / √3) (2/√2) = 6/√6

Tako bo skupna površina piramide enaka
S = 3√3 + 3 * 6/√6
S = 3√3 + 18/√6

Odgovori: 3√3 + 18/√6

Problem 2. Poiščite stransko površino pravilne piramide

rešitev.

Ker je osnova pravilne trikotne piramide enakostranični trikotnik, je AO polmer krožnice, ki je opisana okoli baze.
(To izhaja iz)

Polmer kroga, urejenega okoli enakostraničnega trikotnika, najdemo iz njegovih lastnosti

Od tod bo dolžina robov pravilne trikotne piramide enaka:
AM 2 = MO 2 + AO 2
višina piramide je znana po pogoju (10 cm), AO = 16√3/3
AM 2 = 100 + 256/3
AM = √(556/3)

Vsaka stranica piramide je enakokraki trikotnik. Območje enakokrakega trikotnika najdemo iz prve formule, predstavljene spodaj

S = 1/2 * 16 sqrt((√(556/3) + 8) (√(556/3) - 8))
S = 8 sqrt ((556/3) - 64)
S = 8 sqrt (364/3)
S = 16 sqrt (91/3)

Ker so vse tri ploskve pravilne piramide enake, bo stranska površina enaka
3S = 48 √(91/3)

odgovor: 48 √(91/3)

Problem 3. Poiščite skupno površino pravilne piramide

Stranica pravilne trikotne piramide je 3 cm, kot med stransko ploskvijo in osnovo piramide pa je 45 stopinj. Poiščite celotno površino piramide.

rešitev.
Ker je piramida pravilna, je na njenem dnu enakostranični trikotnik. Zato je površina baze enaka


Torej = 9 * √3/4

Da bi našli površino stranske ploskve, izračunamo višino KM. Glede na nalogo je kot OKM 45 stopinj.
Tako:
OK / MK = cos 45
Izkoristimo

Površina piramide. V tem članku si bomo ogledali težave z običajnimi piramidami. Naj vas spomnim, da je pravilna piramida piramida, katere osnova je pravilen mnogokotnik, vrh piramide je projiciran v središče tega mnogokotnika.

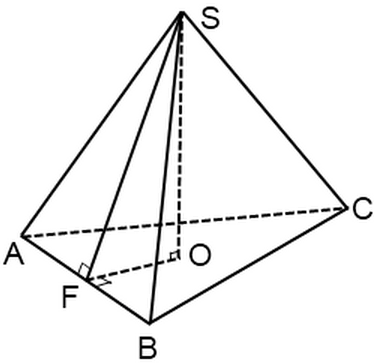
Stranska stran takšne piramide je enakokraki trikotnik.Višina tega trikotnika, potegnjena iz vrha pravilne piramide, se imenuje apotem, SF - apotem:

V vrsti problema, ki je predstavljen spodaj, morate najti površino celotne piramide ali površino njene stranske površine. Na blogu je bilo že obravnavanih več težav s pravilnimi piramidami, kjer se je pojavilo vprašanje iskanja elementov (višina, osnovni rob, stranski rob).

V nalogah enotnega državnega izpita se praviloma upoštevajo pravilne trikotne, štirikotne in šesterokotne piramide. Pri navadnih peterokotnih in sedemkotnih piramidah nisem opazil nobenih težav.

Formula za površino celotne površine je preprosta - najti morate vsoto površine osnove piramide in površine njene stranske površine:

Razmislimo o nalogah:

Strani osnove pravilne štirikotne piramide so 72, stranski robovi pa 164. Poiščite površino te piramide.

Površina piramide je enaka vsoti površin stranske površine in osnove:

* Stranska ploskev je sestavljena iz štirih enako velikih trikotnikov. Osnova piramide je kvadrat.

Ploščino stranice piramide lahko izračunamo z:

Tako je površina piramide:

Odgovor: 28224

Strani osnove pravilne šesterokotne piramide so enake 22, stranski robovi so enaki 61. Poiščite stransko površino te piramide.

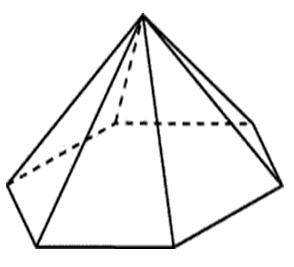
Osnova pravilne šesterokotne piramide je pravilni šesterokotnik.

Stranska površina te piramide je sestavljena iz šestih območij enakih trikotnikov s stranicami 61,61 in 22:

Poiščimo površino trikotnika s Heronovo formulo:

Tako je bočna površina:

Odgovor: 3240

*V zgoraj predstavljenih težavah je mogoče površino stranske ploskve najti z drugo formulo trikotnika, vendar morate za to izračunati apotem.

27155. Poiščite površino pravilne štirikotne piramide, katere osnovne stranice so 6 in višina 4.

Da bi našli površino piramide, moramo poznati površino osnove in površino stranske površine:

Površina osnove je 36, saj je kvadrat s stranico 6.

Stranska površina je sestavljena iz štirih ploskev, ki so enaki trikotniki. Če želite najti območje takšnega trikotnika, morate poznati njegovo osnovo in višino (apotem):

*Ploščina trikotnika je enaka polovici zmnožka osnove in na to osnovo narisane višine.

Osnova je znana, enaka je šest. Poiščimo višino. Razmislite o pravokotnem trikotniku (označeno rumeno):

En krak je enak 4, ker je to višina piramide, drugi je enak 3, ker je enak polovici roba osnove. Hipotenuzo lahko najdemo s pomočjo Pitagorovega izreka:

To pomeni, da je površina stranske površine piramide:

Tako je površina celotne piramide:

Odgovor: 96

27069. Strani osnove pravilne štirikotne piramide so enake 10, stranski robovi so enaki 13. Poiščite površino te piramide.

27070. Strani osnove pravilne šesterokotne piramide so enake 10, stranski robovi so enaki 13. Poiščite stransko površino te piramide.

Obstajajo tudi formule za stransko površino pravilne piramide. V pravilni piramidi je osnova pravokotna projekcija stranske ploskve, torej:

p- osnovni obod, l- apotem piramide

*Ta formula temelji na formuli za ploščino trikotnika.

Če želite izvedeti več o tem, kako so te formule izpeljane, ne zamudite, spremljajte objavo člankov.To je vse. Srečno!

S spoštovanjem, Alexander Krutitskikh.

P.S: Hvaležen bi bil, če bi mi povedali o spletnem mestu na družbenih omrežjih.

Preden preučite vprašanja o tej geometrijski figuri in njenih lastnostih, morate razumeti nekaj izrazov. Ko človek sliši za piramido, si predstavlja ogromne zgradbe v Egiptu. Takole izgledajo najbolj preprosti. Vendar so v različnih vrstah in oblikah, kar pomeni, da bo formula za izračun geometrijskih oblik drugačna.

Piramida - geometrijska figura, ki označuje in predstavlja več obrazov. V bistvu je to isti polieder, na dnu katerega leži mnogokotnik, na straneh pa so trikotniki, ki se povezujejo na eni točki - oglišče. Figura je na voljo v dveh glavnih vrstah:

• pravilno;
• okrnjena.

V prvem primeru je osnova pravilen mnogokotnik. Tu so vse stranske površine enake med seboj in samo figuro bodo zadovoljili oko perfekcionista.

V drugem primeru sta dve bazi - velika na samem dnu in majhna med vrhom, ki ponavlja obliko glavnega. Z drugimi besedami, prisekana piramida je polieder s prerezom, ki je vzporeden z osnovo.

Izrazi in simboli

Ključni pogoji:

• Pravilni (enakostranični) trikotnik- lik s tremi enakimi koti in enakimi stranicami. V tem primeru so vsi koti 60 stopinj. Slika je najpreprostejši izmed pravilnih poliedrov. Če ta številka leži na dnu, se bo takšen polieder imenoval navaden trikotnik. Če je osnova kvadrat, se piramida imenuje pravilna štirikotna piramida.
• Vertex– najvišja točka, kjer se stikata robova. Višino vrha tvori ravna črta, ki poteka od vrha do dna piramide.
• Edge– ena od ravnin mnogokotnika. Lahko je v obliki trikotnika pri trikotni piramidi ali v obliki trapeza pri prisekani piramidi.
• Razdelek- ravna figura, ki je nastala kot posledica disekcije. Ne smemo ga zamenjevati z odsekom, saj odsek prikazuje tudi, kaj je za odsekom.
• Apotema- segment, narisan od vrha piramide do njene osnove. To je tudi višina obraza, kjer se nahaja druga višinska točka. Ta definicija velja le v povezavi s pravilnim poliedrom. Na primer, če to ni okrnjena piramida, bo obraz trikotnik. V tem primeru bo višina tega trikotnika postala apotem.

Površinske formule

Poiščite stransko površino piramide katero koli vrsto je mogoče narediti na več načinov. Če slika ni simetrična in je mnogokotnik z različnimi stranicami, potem je v tem primeru lažje izračunati celotno površino skozi celoto vseh površin. Z drugimi besedami, izračunati morate površino vsake ploskve in ju sešteti.

Odvisno od tega, kateri parametri so znani, bodo morda potrebne formule za izračun kvadrata, trapeza, poljubnega štirikotnika itd. Same formule v različnih primerih bo imel tudi razlike.

V primeru pravilne postave je iskanje območja veliko lažje. Dovolj je poznati le nekaj ključnih parametrov. V večini primerov so izračuni potrebni posebej za takšne številke. Zato bodo ustrezne formule podane spodaj. V nasprotnem primeru bi morali vse izpisati na več straneh, kar bi vas samo zmotilo in zmedlo.

Osnovna formula za izračun Bočna površina pravilne piramide bo imela naslednjo obliko:

S=½ Pa (P je obseg osnove in je apotem)

Poglejmo en primer. Polieder ima osnovo z odseki A1, A2, A3, A4, A5, vsi pa naj bodo enaki 5 cm. Ker je vseh pet ploskev baze enakih, jo lahko najdete takole: P = 5 * 10 = 50 cm Nato uporabimo osnovno formulo: S = ½ * 50 * 5 = 125 cm na kvadrat.

Stranska površina pravilne trikotne piramide najlažje izračunati. Formula izgleda takole:

S =½* ab *3, kjer je a apotem, b je ploskev osnove. Faktor tri tukaj pomeni število ploskev baze, prvi del pa je površina stranske površine. Poglejmo si primer. Podan je lik z apotemo 5 cm in osnovnim robom 8 cm. Izračunamo: S = 1/2*5*8*3=60 cm na kvadrat.

Bočna površina prisekane piramide Malo težje je izračunati. Formula je videti takole: S =1/2*(p_01+ p_02)*a, kjer sta p_01 in p_02 obsega baz in je apotem. Poglejmo si primer. Predpostavimo, da sta za štirikotno figuro dimenzije stranic baz 3 in 6 cm, apotem pa 4 cm.

Tukaj morate najprej najti obode baz: р_01 =3*4=12 cm; r_02=6*4=24 cm. Ostaja, da nadomestimo vrednosti v glavno formulo in dobimo: S =1/2*(12+24)*4=0,5*36*4=72 cm na kvadrat.

Tako lahko najdete stransko površino pravilne piramide katere koli kompleksnosti. Moral bi biti previden in ne zamenjati te izračune s skupno površino celotnega poliedra. In če morate to še vedno storiti, preprosto izračunajte površino največje osnove poliedra in jo dodajte površini stranske površine poliedra.

Video

Ta videoposnetek vam bo pomagal utrditi informacije o tem, kako najti stransko površino različnih piramid.

Niste dobili odgovora na svoje vprašanje? Predlagajte temo avtorjem.

Vemo, kaj je stožec, poskusimo najti njegovo površino. Zakaj morate rešiti tako težavo? Na primer, morate razumeti, koliko testa bo šlo za izdelavo vafeljskega korneta? Ali koliko opek je potrebnih za izdelavo opečne grajske strehe?

Merjenje bočne površine stožca preprosto ni mogoče. Toda predstavljajmo si isti rog, ovit v blago. Če želite najti površino kosa blaga, ga morate razrezati in položiti na mizo. Rezultat je ploščat lik, lahko poiščemo njegovo ploščino.

riž. 1. Odsek stožca vzdolž generatrike

Enako storimo s stožcem. "Odrežemo" njegovo stransko površino vzdolž poljubne generatrise, na primer (glej sliko 1).

Zdaj "odvijmo" stransko površino na ravnino. Dobimo sektor. Središče tega sektorja je vrh stožca, polmer sektorja je enak generatrisi stožca, dolžina njegovega loka pa sovpada z obsegom osnove stožca. Takšen sektor se imenuje razvoj stranske površine stožca (glej sliko 2).

riž. 2. Razvoj stranske površine

riž. 3. Merjenje kota v radianih

Poskusimo poiskati območje sektorja z uporabo razpoložljivih podatkov. Najprej uvedemo zapis: naj bo kot na vrhu sektorja v radianih (glej sliko 3).

Pri težavah se bomo morali pogosto ukvarjati s kotom na vrhu zamaha. Za zdaj poskusimo odgovoriti na vprašanje: ali se ta kot ne more izkazati za več kot 360 stopinj? Se pravi, ali se ne bi izkazalo, da bi se pometanje prekrivalo? Seveda ne. Dokažimo to matematično. Pustite, da se skeniranje "superponira" nase. To pomeni, da je dolžina pometnega loka večja od dolžine kroga polmera . Toda, kot že omenjeno, je dolžina pometnega loka dolžina kroga polmera . In polmer osnove stožca je seveda manjši od na primer generatrise, ker je krak pravokotnega trikotnika manjši od hipotenuze

Potem se spomnimo dveh formul iz tečaja planimetrije: dolžina loka. Območje sektorja: .

V našem primeru vlogo igra generator , dolžina loka pa je enaka obsegu osnove stožca, tj. Imamo:

Končno dobimo: .

Skupaj s stransko površino je mogoče najti tudi skupno površino. Če želite to narediti, dodajte območje podnožja na območje stranske površine. Toda osnova je krog s polmerom, katerega površina je po formuli enaka .

Končno imamo: , kjer je polmer osnove valja, je generatrisa.

Rešimo nekaj nalog z uporabo danih formul.

riž. 4. Zahtevani kot

Primer 1. Razvoj stranske površine stožca je sektor s kotom na vrhu. Poiščite ta kot, če je višina stožca 4 cm in polmer osnove 3 cm (glej sliko 4).

riž. 5. Pravokotni trikotnik, ki tvori stožec

Prvi korak, v skladu s Pitagorovim izrekom, je iskanje generatorja: 5 cm (glej sliko 5). Naprej, to vemo .

Primer 2. Površina osnega prereza stožca je enaka , višina je enaka . Poiščite skupno površino (glej sliko 6).