Linear angle of a dihedral angle in a pyramid. Dihedral angles and formula for calculating them. Dihedral angle at the base of a quadrangular regular pyramid. Protection of personal information
CHAPTER ONE STRAIGHT AND PLANES
V. DIHEDRAL ANGLES, RIGHT ANGLE WITH A PLANE,
ANGLE OF TWO CROSSING RIGHT STRAIGHTS, POLYHEDAL ANGLES
Dihedral angles
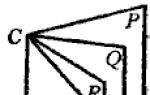
38. Definitions. The part of the plane lying on one side of any straight line lying in this plane is called half-plane. A figure formed by two half-planes (P and Q, Fig. 26) emanating from one straight line (AB) is called dihedral angle. Direct AB is called edge, and the half-planes P and Q - parties or edges dihedral angle.
Such an angle is usually designated by two letters placed at its edge (dihedral angle AB). But if at one edge there are several dihedral angles, then each of them is designated by four letters, of which the middle two are at the edge, and the outer two are at the faces (for example, dihedral angle SCDR) (Fig. 27).

If from an arbitrary point D edges AB (Fig. 28) are drawn on each face perpendicular to the edge, then the angle CDE formed by them is called linear angle dihedral angle.

The magnitude of a linear angle does not depend on the position of its vertex on the edge. Thus, linear angles CDE and C 1 D 1 E 1 are equal because their sides are respectively parallel and in the same direction.
The plane of a linear angle is perpendicular to the edge, since it contains two lines perpendicular to it. Therefore, to obtain a linear angle, it is enough to intersect the face of a given dihedral angle with a plane perpendicular to the edge, and consider the resulting angle in this plane.
39. Equality and inequality of dihedral angles. Two dihedral angles are considered equal if they can be combined when inserted; otherwise, whichever dihedral angle is considered to be the smaller one will form part of the other angle.
Like angles in planimetry, dihedral angles can be adjacent, vertical etc.
If two adjacent dihedral angles are equal to each other, then each of them is called right dihedral angle.
Theorems. 1) Equal dihedral angles correspond to equal linear angles.
2) A larger dihedral angle corresponds to a larger linear angle.
Let PABQ, and P 1 A 1 B 1 Q 1 (Fig. 29) be two dihedral angles. We insert angle A 1 B 1 into angle AB so that edge A 1 B 1 coincides with edge AB and face P 1 with face P.

Then if these dihedral angles are equal, then face Q 1 will coincide with face Q; if angle A 1 B 1 is less than angle AB, then face Q 1 will take some position inside the dihedral angle, for example Q 2.
Having noticed this, let’s take some point B on a common edge and draw a plane R through it, perpendicular to the edge. From the intersection of this plane with the faces of the dihedral angles, linear angles are obtained. It is clear that if the dihedral angles coincide, then they will have the same linear angle CBD; if the dihedral angles do not coincide, if, for example, face Q 1 takes the position Q 2, then the larger dihedral angle will have a larger linear angle (namely: / CBD > / C 2 BD).
40. Converse theorems. 1) Equal linear angles correspond to equal dihedral angles.
2) A larger linear angle corresponds to a larger dihedral angle .
These theorems can be easily proven by contradiction.
41. Consequences. 1) A right dihedral angle corresponds to a right linear angle, and vice versa.

Let (Fig. 30) the dihedral angle PABQ be straight. This means that it is equal to the adjacent angle QABP 1. But in this case, the linear angles CDE and CDE 1 are also equal; and since they are adjacent, each of them must be straight. Conversely, if adjacent linear angles CDE and CDE 1 are equal, then adjacent dihedral angles are equal, i.e., each of them must be straight.
2) All right dihedral angles are equal, because their linear angles are equal .
Likewise, it is easy to prove that:
3) Vertical dihedral angles are equal.
4) Dihedral angles with respectively parallel and identically (or oppositely) directed edges are equal.
5) If we take as a unit of dihedral angles a dihedral angle that corresponds to a unit of linear angles, then we can say that a dihedral angle is measured by its linear angle.
To use presentation previews, create a Google account and log in to it: https://accounts.google.com
Slide captions:
DIHEDRAL ANGLE Mathematics teacher GOU secondary school No. 10 Eremenko M.A.
Main objectives of the lesson: Introduce the concept of a dihedral angle and its linear angle. Consider tasks for the application of these concepts.
Definition: A dihedral angle is a figure formed by two half-planes with a common boundary straight line.
The magnitude of a dihedral angle is the magnitude of its linear angle. AF ⊥ CD BF ⊥ CD AFB - linear dihedral angle ACD B
Let us prove that all linear angles of a dihedral angle are equal to each other. Let's consider two linear angles AOB and A 1 OB 1. Rays OA and OA 1 lie on the same face and are perpendicular to OO 1, so they are codirectional. Beams OB and OB 1 are also co-directed. Therefore, ∠ AOB = ∠ A 1 OB 1 (like angles with co-directed sides).
Examples of dihedral angles:
Definition: The angle between two intersecting planes is the smallest of the dihedral angles formed by these planes.
Task 1: In cube A ... D 1, find the angle between planes ABC and CDD 1. Answer: 90 o.
Problem 2: In cube A ... D 1, find the angle between planes ABC and CDA 1. Answer: 45 o.
Problem 3: In cube A ... D 1, find the angle between planes ABC and BDD 1. Answer: 90 o.
Problem 4: In the cube A ... D 1, find the angle between the planes ACC 1 and BDD 1. Answer: 90 o.
Problem 5: In cube A ... D 1, find the angle between planes BC 1 D and BA 1 D. Solution: Let O be the midpoint of B D. A 1 OC 1 – the linear angle of the dihedral angle A 1 B D C 1.
Problem 6: In the tetrahedron DABC all edges are equal, point M is the middle of edge AC. Prove that ∠ DMB is the linear angle of the dihedral angle BACD .
Solution: Triangles ABC and ADC are regular, therefore, BM ⊥ AC and DM ⊥ AC and hence ∠ DMB is the linear angle of dihedral angle DACB.
Problem 7: From vertex B of triangle ABC, side AC of which lies in the plane α, a perpendicular BB 1 is drawn to this plane. Find the distance from point B to the straight line AC and to the plane α, if AB=2, ∠ВАС=150 0 and the dihedral angle ВАСВ 1 is equal to 45 0.
Solution: ABC is an obtuse triangle with obtuse angle A, therefore the base of the altitude BC lies on the extension of side AC. VC – distance from point B to AC. BB 1 – distance from point B to plane α
2) Since AC ⊥BK, then AC⊥KB 1 (by the theorem inverse to the theorem about three perpendiculars). Therefore, ∠VKV 1 is the linear angle of the dihedral angle BASV 1 and ∠VKV 1 =45 0 . 3) ∆VAK: ∠A=30 0, VK=VA·sin 30 0, VK =1. ∆ВКВ 1: ВВ 1 =ВК· sin 45 0 , ВВ 1 =
In geometry, two important characteristics are used to study figures: the lengths of the sides and the angles between them. In the case of spatial figures, dihedral angles are added to these characteristics. Let's look at what it is, and also describe the method for determining these angles using the example of a pyramid.
The concept of dihedral angle
Everyone knows that two intersecting lines form a certain angle with the vertex at the point of their intersection. This angle can be measured using a protractor or you can use trigonometric functions to calculate it. An angle formed by two right angles is called linear.
Now imagine that in three-dimensional space there are two planes that intersect in a straight line. They are shown in the picture.
A dihedral angle is the angle between two intersecting planes. Just like linear, it is measured in degrees or radians. If to any point on the line along which the planes intersect, we restore two perpendiculars lying in these planes, then the angle between them will be the desired dihedral. The easiest way to determine this angle is to use the equations of planes in general form.
Equation of planes and formula for the angle between them
The equation of any plane in space is generally written as follows:
A × x + B × y + C × z + D = 0.
Here x, y, z are the coordinates of points belonging to the plane, the coefficients A, B, C, D are some known numbers. The convenience of this equality for calculating dihedral angles is that it explicitly contains the coordinates of the direction vector of the plane. We will denote it n¯. Then:

Vector n¯ is perpendicular to the plane. The angle between two planes is equal to the angle between their n 1 ¯ and n 2 ¯. It is known from mathematics that the angle formed by two vectors is uniquely determined from their scalar product. This allows us to write a formula for calculating the dihedral angle between two planes:
φ = arccos (|(n 1 ¯ × n 2 ¯)| / (|n 1 ¯| × |n 2 ¯|)).
If we substitute the coordinates of the vectors, the formula will be written explicitly:
φ = arccos (|A 1 × A 2 + B 1 × B 2 + C 1 × C 2 | / (√(A 1 2 + B 1 2 + C 1 2) × √(A 2 2 + B 2 2 + C 2 2))).
The modulus sign in the numerator is used to define only the acute angle, since the dihedral angle is always less than or equal to 90 o.
Pyramid and its corners

A pyramid is a figure that is formed by one n-gon and n triangles. Here n is an integer equal to the number of sides of the polygon that is the base of the pyramid. This spatial figure is a polyhedron or polyhedron, since it consists of flat faces (sides).
Pyramid polyhedrons can be of two types:
- between the base and the side (triangle);
- between the two sides.
If we are considering a regular pyramid, then the named angles for it are not difficult to determine. To do this, using the coordinates of three known points, you should create an equation of the planes, and then use the formula given in the paragraph above for the angle φ.
Below we give an example in which we show how to find dihedral angles at the base of a regular quadrangular pyramid.
Quadrangular and the angle at its base
Let us assume that we are given a regular pyramid with a square base. The length of the side of the square is a, the height of the figure is h. Let's find the angle between the base of the pyramid and its side.

Let's place the origin of the coordinate system at the center of the square. Then the coordinates of points A, B, C, D shown in the figure will be equal:
A = (a/2; -a/2; 0);
B = (a/2; a/2; 0);
C = (-a/2; a/2; 0);
Let's consider the planes ACB and ADB. Obviously, the direction vector n 1 ¯ for the plane ACB will be equal to:
To determine the direction vector n 2 ¯ of the ADB plane, we proceed as follows: we find arbitrary two vectors that belong to it, for example, AD¯ and AB¯, then we calculate their vector product. Its result will give the coordinates n 2 ¯. We have:
AD¯ = D - A = (0; 0; h) - (a/2; -a/2; 0) = (-a/2; a/2; h);
AB¯ = B - A = (a/2; a/2; 0) - (a/2; -a/2; 0) = (0; a; 0);
n 2 ¯ = = [(-a/2; a/2; h) × (0; a; 0)] = (-a × h; 0; -a 2 /2).
Since multiplying and dividing a vector by a number does not change its direction, we transform the resulting n 2 ¯ by dividing its coordinates by -a, we get:
We have defined the direction vectors n 1 ¯ and n 2 ¯ for the base planes ACB and side plane ADB. It remains to use the formula for the angle φ:
φ = arccos (|(n 1 ¯ × n 2 ¯)| / (|n 1 ¯| × |n 2 ¯|)) = arccos (a / (2 × √h 2 + a 2 /4)).
Let's transform the resulting expression and rewrite it like this:
φ = arccos (a / √(a 2 + 4 × h 2)).
We have obtained a formula for the dihedral angle at the base for a regular quadrangular pyramid. Knowing the height of the figure and the length of its side, you can calculate the angle φ. For example, for the Cheops pyramid, the base side of which is 230.4 meters, and the initial height was 146.5 meters, the angle φ will be equal to 51.8 o.

You can also determine the dihedral angle for a quadrangular regular pyramid using the geometric method. To do this, it is enough to consider a right triangle formed by the height h, half the length of the base a/2 and the apothem of an isosceles triangle.
Maintaining your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please review our privacy practices and let us know if you have any questions.
Collection and use of personal information
Personal information refers to data that can be used to identify or contact a specific person.
You may be asked to provide your personal information at any time when you contact us.
Below are some examples of the types of personal information we may collect and how we may use such information.
What personal information do we collect:
- When you submit an application on the site, we may collect various information, including your name, phone number, email address, etc.
How we use your personal information:
- The personal information we collect allows us to contact you with unique offers, promotions and other events and upcoming events.
- From time to time, we may use your personal information to send important notices and communications.
- We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
- If you participate in a prize draw, contest or similar promotion, we may use the information you provide to administer such programs.
Disclosure of information to third parties
We do not disclose the information received from you to third parties.
Exceptions:
- If necessary - in accordance with the law, judicial procedure, in legal proceedings, and/or on the basis of public requests or requests from government bodies in the Russian Federation - to disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public importance purposes.
- In the event of a reorganization, merger, or sale, we may transfer the personal information we collect to the applicable successor third party.
Protection of personal information
We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as unauthorized access, disclosure, alteration and destruction.
Respecting your privacy at the company level
To ensure that your personal information is secure, we communicate privacy and security standards to our employees and strictly enforce privacy practices.
Back Forward
Attention! Slide previews are for informational purposes only and may not represent all of the presentation's features. If you are interested in this work, please download the full version.
Lesson objectives: introduce the concept of a dihedral angle and its linear angle;
Lesson progress
I. Organizational moment.
Inform the topic of the lesson, formulate the objectives of the lesson.
II. Updating students' knowledge (slide 2, 3).
1. Preparation for studying new material.
What is an angle in a plane called?
What is the angle between lines in space called?
What is the angle between a straight line and a plane called?
State the three perpendicular theorem
III. Learning new material.
- The concept of dihedral angle.
A figure formed by two half-planes passing through a line MN is called a dihedral angle (slide 4).
Half-planes are faces, straight line MN is an edge of a dihedral angle.
What objects in everyday life have the shape of a dihedral angle? (Slide 5)
- The angle between the planes АСН and СНD is the dihedral angle АСНD, where СН is an edge. Points A and D lie on the faces of this angle. Angle AFD is the linear angle of the dihedral angle ACHD (slide 6).
- Algorithm for constructing a linear angle (slide 7).
1 way. On the edge, take any point O and draw perpendiculars to this point (PO DE, KO DE) to obtain the angle ROK - linear.
Method 2. In one half-plane, take point K and drop two perpendiculars from it to another half-plane and an edge (KO and KR), then by the inverse TTP theorem PODE
- All linear angles of a dihedral angle are equal (slide 8). Proof: rays OA and O 1 A 1 are co-directed, rays OB and O 1 B 1 are also co-directed, angles BOA and B 1 O 1 A 1 are equal as angles with co-directed sides.
- The degree measure of a dihedral angle is the degree measure of its linear angle (slide 9).
IV. Consolidation of the studied material.
- Solving problems (orally using ready-made drawings). (Slides 10-12)
1. RAVS – pyramid; angle ACB is equal to 90°, straight line PB is perpendicular to plane ABC. Prove that angle RSV is a linear angle of a dihedral angle with
2. RAVS - pyramid; AB = BC, D is the middle of the segment AC, straight line PB is perpendicular to the plane ABC. Prove that angle PDB is a linear angle of a dihedral angle with edge AC.
3. PABCD – pyramid; straight line PB is perpendicular to plane ABC, BC is perpendicular to DC. Prove that angle RKB is a linear angle of a dihedral angle with edge CD.
- Problems on constructing a linear angle (slides 13-14).
1. Construct a linear angle of a dihedral angle with an edge AC, if in the pyramid RABC the face ABC is a regular triangle, O is the point of intersection of the medians, the straight line PO is perpendicular to the plane ABC
2. Given a rhombus ABCD. Straight line RS is perpendicular to plane ABCD.
Construct the linear angle of a dihedral angle with edge ВD and the linear angle of a dihedral angle with edge AD.
- Computational task. (Slide 15)
In parallelogram ABCD, angle ADC is equal to 120 0, AD = 8 cm,
DC = 6 cm, straight line RS is perpendicular to plane ABC, RS = 9 cm.
Find the size of the dihedral angle with edge AD and the area of the parallelogram.
V. Homework (slide 16).
P. 22, No. 168, 171.
Literature used:
- Geometry 10-11 L.S.Atanasyan.
- System of problems on the topic “Dihedral angles” by M.V. Sevostyanova (Murmansk), magazine Mathematics at school 198...