13 அதிவேக செயல்பாடு, அதன் பண்புகள் மற்றும் வரைபடம். பாடம் “அதிவேக செயல்பாடு, அதன் பண்புகள் மற்றும் வரைபடம்

x=2 என்ற மாறியின் பல்வேறு பகுத்தறிவு மதிப்புகளுக்கான வெளிப்பாட்டின் மதிப்பைக் கண்டுபிடிப்போம்; 0; -3; -

x என்ற மாறிக்கு எந்த எண்ணை மாற்றினாலும், இந்த வெளிப்பாட்டின் மதிப்பை நாம் எப்போதும் காணலாம் என்பதை நினைவில் கொள்க. இதன் பொருள், விகிதமுறு எண்களின் தொகுப்பில் வரையறுக்கப்பட்ட ஒரு அதிவேக செயல்பாட்டை (E என்பது x இன் சக்திக்கு மூன்றுக்கு சமம்) பரிசீலிக்கிறோம்: .

அதன் மதிப்புகளின் அட்டவணையை தொகுத்து இந்த செயல்பாட்டின் வரைபடத்தை உருவாக்குவோம்.

இந்த புள்ளிகள் வழியாக ஒரு மென்மையான கோட்டை வரைவோம் (படம் 1)

இந்த செயல்பாட்டின் வரைபடத்தைப் பயன்படுத்தி, அதன் பண்புகளைக் கருத்தில் கொள்வோம்:

3. வரையறையின் முழுப் பகுதியிலும் அதிகரிக்கிறது.

1. பூஜ்ஜியத்திலிருந்து கூட்டல் முடிவிலி வரையிலான மதிப்புகளின் வரம்பு.

8. செயல்பாடு குவிந்த கீழ்நோக்கி உள்ளது.

ஒரு ஒருங்கிணைப்பு அமைப்பில் செயல்பாடுகளின் வரைபடங்களை உருவாக்கினால்; y=(y என்பது x-ன் சக்திக்கு இரண்டுக்கு சமம், y என்பது x-ன் சக்திக்கு ஐந்து, y என்பது x-ன் சக்திக்கு ஏழு சமம்), அப்போது அவை y= போன்ற பண்புகளைக் கொண்டிருப்பதைக் காணலாம். (y என்பது x இன் சக்திக்கு மூன்றுக்கு சமம்) (படம் .2), அதாவது, y = (a என்பது x சக்திக்கு சமம், ஒன்றுக்கு மேல்) வடிவத்தின் அனைத்து செயல்பாடுகளும் அத்தகைய பண்புகளைக் கொண்டிருக்கும்.

செயல்பாட்டைத் திட்டமிடுவோம்:

1. அதன் மதிப்புகளின் அட்டவணையை தொகுத்தல்.

பெறப்பட்ட புள்ளிகளை ஒருங்கிணைப்பு விமானத்தில் குறிப்போம்.

இந்த புள்ளிகள் வழியாக ஒரு மென்மையான கோட்டை வரைவோம் (படம் 3).

இந்த செயல்பாட்டின் வரைபடத்தைப் பயன்படுத்தி, அதன் பண்புகளைக் குறிப்பிடுகிறோம்:

1. வரையறையின் களம் என்பது அனைத்து உண்மையான எண்களின் தொகுப்பாகும்.

2. இரட்டையோ அல்லது இரட்டையோ அல்ல.

3. வரையறையின் முழு களத்திலும் குறைகிறது.

4. பெரிய அல்லது சிறிய மதிப்புகள் இல்லை.

5.கீழே வரம்பிடப்பட்டுள்ளது, ஆனால் மேலே வரையறுக்கப்படவில்லை.

6. வரையறையின் முழு களத்திலும் தொடர்கிறது.

7. பூஜ்ஜியத்திலிருந்து கூட்டல் முடிவிலி வரையிலான மதிப்புகளின் வரம்பு.

8. செயல்பாடு குவிந்த கீழ்நோக்கி உள்ளது.

இதேபோல், ஒரு ஒருங்கிணைப்பு அமைப்பில் செயல்பாடுகளின் வரைபடங்களை உருவாக்கினால்; y = (y என்பது x இன் சக்திக்கு ஒரு பாதிக்கு சமம், y என்பது x இன் சக்திக்கு ஐந்தில் ஒரு பங்கு, y என்பது x இன் சக்திக்கு ஏழில் ஒரு பங்குக்கு சமம்), பின்னர் அவர்கள் இருப்பதை நீங்கள் கவனிக்கலாம் அதே பண்புகள் y = (y என்பது சக்தி x க்கு மூன்றில் ஒரு பங்குக்கு சமம் (படம் 4), அதாவது, y = வடிவத்தின் அனைத்து செயல்பாடுகளும் (y என்பது x சக்திக்கு a ஆல் வகுக்கப்படும், உடன் பூஜ்ஜியத்தை விட பெரியது ஆனால் ஒன்றுக்கு குறைவானது) அத்தகைய பண்புகளைக் கொண்டிருக்கும்.

ஒரு ஒருங்கிணைப்பு அமைப்பில் செயல்பாடுகளின் வரைபடங்களை உருவாக்குவோம்

இதன் பொருள் y=y= சார்புகளின் வரைபடங்களும் சமச்சீராக இருக்கும் (y என்பது x மற்றும் y இன் சக்திக்கு சமம். ஒன்றுக்கு சமம், a ஆல் வகுக்கப்படும் சக்தி x) a இன் அதே மதிப்புக்கு.

அதிவேக செயல்பாட்டை வரையறுத்து அதன் முக்கிய பண்புகளைக் குறிப்பிடுவதன் மூலம் சொல்லப்பட்டதை சுருக்கமாகக் கூறுவோம்:

வரையறை: y= வடிவத்தின் ஒரு சார்பு, அங்கு (y என்பது x சக்திக்கு சமம், இதில் a நேர்மறை மற்றும் ஒன்றிலிருந்து வேறுபட்டது), இது ஒரு அதிவேகச் சார்பு எனப்படும்.

அதிவேக சார்பு y= மற்றும் சக்தி சார்பு y=, a=2,3,4,.... ஆகியவற்றுக்கு இடையே உள்ள வேறுபாடுகளை நினைவில் கொள்வது அவசியம். கேட்கக்கூடிய மற்றும் பார்வை. அதிவேக செயல்பாடு எக்ஸ்ஒரு பட்டம், மற்றும் சக்தி செயல்பாடு எக்ஸ்அடிப்படையாக உள்ளது.

எடுத்துக்காட்டு1: சமன்பாட்டைத் தீர்க்கவும் (மூன்று சக்தி x ஒன்பதுக்கு சமம்)

(Y என்பது X இன் சக்திக்கு மூன்று மற்றும் Y என்பது ஒன்பதுக்கு சமம்) படம் 7

அவற்றுக்கு ஒரு பொதுவான புள்ளி M (2;9) (இரண்டு ஆயத்தொலைவுகளுடன்; ஒன்பது) இருப்பதைக் கவனியுங்கள், அதாவது புள்ளியின் abscissa மூலமாக இருக்கும் கொடுக்கப்பட்ட சமன்பாடு. அதாவது, சமன்பாட்டில் x = 2 என்ற ஒற்றை வேர் உள்ளது.

எடுத்துக்காட்டு 2: சமன்பாட்டைத் தீர்க்கவும்

ஒரு ஒருங்கிணைப்பு அமைப்பில், y= செயல்பாட்டின் இரண்டு வரைபடங்களை உருவாக்குவோம் (y என்பது x இன் சக்திக்கு ஐந்து மற்றும் y என்பது இருபத்தி ஐந்தில் ஒன்றுக்கு சமம்) படம் 8. வரைபடங்கள் T (-2; (-2; (ஆயங்கள் மைனஸ் இரண்டு; ஒன்று இருபத்தி-ஐந்தாவது) உடன் te) வெட்டுகின்றன. இதன் பொருள் சமன்பாட்டின் வேர் x = -2 (எண் கழித்தல் இரண்டு) ஆகும்.

எடுத்துக்காட்டு 3: சமத்துவமின்மையைத் தீர்ப்பது

ஒரு ஒருங்கிணைப்பு அமைப்பில் y= செயல்பாட்டின் இரண்டு வரைபடங்களை உருவாக்குவோம்

(Y என்பது X இன் சக்திக்கு மூன்று மற்றும் Y என்பது இருபத்தேழுக்கு சமம்).

படம்.9 செயல்பாட்டின் வரைபடம் y=at செயல்பாட்டின் வரைபடத்திற்கு மேலே அமைந்துள்ளது

x எனவே, சமத்துவமின்மைக்கான தீர்வு இடைவெளி (மைனஸ் முடிவிலியிலிருந்து மூன்று வரை)

எடுத்துக்காட்டு 4: சமத்துவமின்மையைத் தீர்க்கவும்

ஒரு ஒருங்கிணைப்பு அமைப்பில், y= செயல்பாட்டின் இரண்டு வரைபடங்களை உருவாக்குவோம் (y என்பது x இன் சக்திக்கு நான்கில் ஒரு பங்கு மற்றும் y என்பது பதினாறுக்கு சமம்). (படம் 10). வரைபடங்கள் K (-2;16) ஒரு புள்ளியில் வெட்டுகின்றன. இதன் பொருள் சமத்துவமின்மைக்கான தீர்வு இடைவெளி (-2; (மைனஸ் இரண்டிலிருந்து பிளஸ் இன்ஃபினிட்டி வரை), y= செயல்பாட்டின் வரைபடம் x இல் செயல்பாட்டின் வரைபடத்திற்குக் கீழே அமைந்துள்ளது.

எங்கள் பகுத்தறிவு பின்வரும் கோட்பாடுகளின் செல்லுபடியை சரிபார்க்க அனுமதிக்கிறது:

தீம் 1: உண்மை என்றால் m=n என்றால் மட்டும்.

தேற்றம் 2: என்றால் உண்மை என்றால் மற்றும் இருந்தால் மட்டும், சமத்துவமின்மை என்றால் மட்டும் உண்மை (படம். *)

தேற்றம் 4: உண்மை என்றால் மற்றும் இருந்தால் மட்டுமே (படம்.**), தேற்றம் 3: உண்மை என்றால் மற்றும் m=n என்றால் மட்டுமே.

எடுத்துக்காட்டு 5: y= செயல்பாட்டை வரைபடமாக்குங்கள்

y= என்ற பட்டத்தின் பண்பைப் பயன்படுத்துவதன் மூலம் செயல்பாட்டை மாற்றியமைப்போம்

கூடுதல் ஒருங்கிணைப்பு அமைப்பை உருவாக்குவோம் புதிய அமைப்புஒருங்கிணைப்புகள், y = செயல்பாட்டின் வரைபடத்தை உருவாக்குவோம் (y என்பது x சக்திக்கு இரண்டுக்கு சமம்) படம் 11.

எடுத்துக்காட்டு 6: சமன்பாட்டைத் தீர்க்கவும்

ஒரு ஒருங்கிணைப்பு அமைப்பில் y= செயல்பாட்டின் இரண்டு வரைபடங்களை உருவாக்குவோம்

(Y என்பது X இன் சக்திக்கு ஏழு மற்றும் Y என்பது எட்டு கழித்தல் X க்கு சமம்) படம் 12.

வரைபடங்கள் ஒரு புள்ளியில் E (1; (e உடன் ஆய ஒன்று; ஏழு) வெட்டும் சமன்பாட்டின் வேர் x = 1 (x ஒன்றுக்கு சமம்).

எடுத்துக்காட்டு 7: சமத்துவமின்மையைத் தீர்க்கவும்

ஒரு ஒருங்கிணைப்பு அமைப்பில் y= செயல்பாட்டின் இரண்டு வரைபடங்களை உருவாக்குவோம்

(y என்பது x மற்றும் i இன் சக்திக்கு நான்கில் ஒரு பங்கிற்கு சமம் x க்கு சமம்பிளஸ் ஐந்து). y=செயல்பாட்டின் வரைபடம் y=x+5 செயல்பாட்டின் வரைபடத்திற்கு கீழே அமைந்துள்ளது, சமத்துவமின்மைக்கான தீர்வு இடைவெளி x (மைனஸ் ஒன்றிலிருந்து கூட்டல் முடிவிலி வரை).

அறிவின் ஹைப்பர் மார்க்கெட் >>கணிதம் >>கணிதம் 10ம் வகுப்பு >>

அதிவேக செயல்பாடு, அதன் பண்புகள் மற்றும் வரைபடம்

2x என்ற வெளிப்பாட்டைக் கருத்தில் கொள்வோம் மற்றும் x மாறியின் பல்வேறு பகுத்தறிவு மதிப்புகளுக்கு அதன் மதிப்புகளைக் கண்டுபிடிப்போம், எடுத்துக்காட்டாக, x = 2;

பொதுவாக, x மாறிக்கு நாம் என்ன பகுத்தறிவு அர்த்தத்தை வழங்கினாலும், 2 x என்ற வெளிப்பாட்டின் தொடர்புடைய எண் மதிப்பை எப்போதும் கணக்கிடலாம். எனவே, நாம் அதிவேகத்தைப் பற்றி பேசலாம் செயல்பாடுகள் y=2 x, பகுத்தறிவு எண்களின் Q தொகுப்பில் வரையறுக்கப்பட்டுள்ளது:

இந்த செயல்பாட்டின் சில அம்சங்களைப் பார்ப்போம்.

சொத்து 1.- செயல்பாடு அதிகரிக்கும். நாங்கள் இரண்டு நிலைகளில் ஆதாரத்தை மேற்கொள்கிறோம்.
முதல் நிலை. r என்பது நேர்மறை விகிதமுறு எண் என்றால், 2 r >1 என்பதை நிரூபிப்போம்.
இரண்டு வழக்குகள் சாத்தியம்: 1) ஆர் - இயற்கை எண், r = n; 2) சாதாரண குறைக்க முடியாதது பின்னம்,

நம்மிடம் உள்ள கடைசி சமத்துவமின்மையின் இடது பக்கத்தில் , மற்றும் வலது பக்கம் 1. அதாவது கடைசி சமத்துவமின்மையை வடிவத்தில் மீண்டும் எழுதலாம்

எனவே, எந்தவொரு சந்தர்ப்பத்திலும், சமத்துவமின்மை 2 r > 1 உள்ளது, இது நிரூபிக்கப்பட வேண்டும்.

இரண்டாம் நிலை. x 1 மற்றும் x 2 எண்களாகவும், x 1 மற்றும் x 2 ஆகவும் இருக்கட்டும்< х2. Составим разность 2 х2 -2 х1 и выполним некоторые ее преобразования:

(x 2 - x 1 என்ற வித்தியாசத்தை r என்ற எழுத்தில் குறிப்பிட்டோம்).

r என்பது நேர்மறை விகிதமுறு எண் என்பதால், முதல் கட்டத்தில் நிரூபிக்கப்பட்டதன் மூலம், 2 r > 1, அதாவது. 2 ஆர் -1 >0. 2x" என்ற எண்ணும் நேர்மறை, அதாவது 2 x-1 (2 Г -1) என்பதும் நேர்மறை. சமத்துவமின்மை 2 Xg -2x" >0.

எனவே, சமத்துவமின்மையிலிருந்து x 1< х 2 следует, что 2х" <2 x2 , а это и означает, что функция у -2х - возрастающая.

சொத்து 2.கீழே இருந்து வரம்புக்குட்பட்டது மற்றும் மேலே இருந்து வரம்பு இல்லை.
கீழே இருந்து செயல்பாட்டின் எல்லையானது சமத்துவமின்மை 2 x >0 இலிருந்து பின்பற்றப்படுகிறது, இது செயல்பாட்டின் வரையறையின் டொமைனில் இருந்து x இன் எந்த மதிப்புகளுக்கும் செல்லுபடியாகும். அதே நேரத்தில், எதுவாக இருந்தாலும் நேர்மறை எண்எதுவாக இருந்தாலும், சமத்துவமின்மை 2 x >M திருப்தி அடையும் வகையில், நீங்கள் எப்போதும் ஒரு அடுக்கு x ஐ தேர்வு செய்யலாம் - இது மேலே இருந்து செயல்பாட்டின் வரம்பற்ற தன்மையை வகைப்படுத்துகிறது. பல உதாரணங்களைத் தருவோம்.

சொத்து 3.சிறிய அல்லது பெரிய மதிப்பு இல்லை.

என்ன இந்த செயல்பாடுமிகப்பெரிய முக்கியத்துவம் இல்லை, வெளிப்படையாக, நாம் இப்போது பார்த்தபடி, அது மேலே இருந்து வரம்பற்றது அல்ல. ஆனால் அது கீழே இருந்து வரம்பிடப்பட்டுள்ளது, ஏன் குறைந்தபட்ச மதிப்பைக் கொண்டிருக்கவில்லை?

2 கிராம் என்று வைத்துக் கொள்வோம் - மிகச்சிறிய மதிப்புசெயல்பாடுகள் (ஆர் - சில பகுத்தறிவு காட்டி) q என்ற பகுத்தறிவு எண்ணை எடுத்துக் கொள்வோம்<г. Тогда в силу возрастания функции у=2 х будем иметь 2 x <2г. А это значит, что 2 r не может служить наименьшим значением функции.

இதெல்லாம் நல்லது, நீங்கள் சொல்கிறீர்கள், ஆனால் y-2 x செயல்பாட்டை ஏன் பகுத்தறிவு எண்களின் தொகுப்பில் மட்டுமே கருதுகிறோம், முழு எண் கோட்டில் அல்லது சில தொடர்ச்சியான இடைவெளியில் மற்ற அறியப்பட்ட செயல்பாடுகளைப் போல ஏன் கருதக்கூடாது? எண் கோடு? எது நம்மைத் தடுக்கிறது? நிலைமையை யோசிப்போம்.

எண் கோட்டில் பகுத்தறிவு மட்டுமல்ல, ஐஆர் உள்ளது பகுத்தறிவு எண்கள். முன்பு படித்த செயல்பாடுகளுக்கு இது எங்களைத் தொந்தரவு செய்யவில்லை. எடுத்துக்காட்டாக, x இன் பகுத்தறிவு மற்றும் பகுத்தறிவற்ற மதிப்புகள் இரண்டிற்கும் y = x2 செயல்பாட்டின் மதிப்புகளை சமமாக எளிதாகக் கண்டறிந்தோம்: கொடுக்கப்பட்ட x மதிப்பை சதுரப்படுத்த இது போதுமானது.

ஆனால் y=2 x செயல்பாட்டில் நிலைமை மிகவும் சிக்கலானது. வாதம் x க்கு ஒரு பகுத்தறிவு அர்த்தம் கொடுக்கப்பட்டால், கொள்கையளவில் x ஐக் கணக்கிடலாம் (பத்தியின் தொடக்கத்திற்கு மீண்டும் செல்லுங்கள், அங்கு நாங்கள் இதைச் செய்தோம்). வாதம் x க்கு பகுத்தறிவற்ற அர்த்தம் கொடுக்கப்பட்டால் என்ன செய்வது? உதாரணமாக, எப்படி கணக்கிடுவது? இது எங்களுக்கு இன்னும் தெரியாது.
கணிதவியலாளர்கள் ஒரு வழியைக் கண்டுபிடித்துள்ளனர்; என்று அவர்கள் நியாயப்படுத்தினர்.

என்பது தெரிந்ததே பகுத்தறிவு எண்களின் வரிசையைக் கவனியுங்கள் - தீமையின்படி ஒரு எண்ணின் தசம தோராயங்கள்:

1; 1,7; 1,73; 1,732; 1,7320; 1,73205; 1,732050; 1,7320508;... .

1.732 = 1.7320, மற்றும் 1.732050 = 1.73205 என்பது தெளிவாகிறது. இதுபோன்ற மறுநிகழ்வுகளைத் தவிர்க்க, 0 என்ற எண்ணுடன் முடிவடையும் வரிசையின் உறுப்பினர்களை நிராகரிக்கிறோம்.

பின்னர் நாம் அதிகரிக்கும் வரிசையைப் பெறுகிறோம்:

1; 1,7; 1,73; 1,732; 1,73205; 1,7320508;... .

அதன்படி, வரிசை அதிகரிக்கிறது

இந்த வரிசையின் அனைத்து விதிமுறைகளும் 22 க்கும் குறைவான நேர்மறை எண்கள், அதாவது. இந்த வரிசை வரையறுக்கப்பட்டுள்ளது. வீயர்ஸ்ட்ராஸின் தேற்றத்தின்படி (§ 30 ஐப் பார்க்கவும்), ஒரு வரிசை அதிகரித்து வரம்பாக இருந்தால், அது ஒன்றிணைகிறது. கூடுதலாக, § 30 இலிருந்து ஒரு வரிசை ஒன்றிணைந்தால், அது ஒரு வரம்புக்கு மட்டுமே செல்கிறது என்பதை அறிவோம். இந்த ஒற்றை வரம்பு எண் வெளிப்பாட்டின் மதிப்பாகக் கருதப்பட வேண்டும் என்று ஒப்புக்கொள்ளப்பட்டது. எண் வெளிப்பாடு 2 இன் தோராயமான மதிப்பைக் கூட கண்டுபிடிப்பது மிகவும் கடினம் என்பது முக்கியமல்ல; இது ஒரு குறிப்பிட்ட எண் என்பது முக்கியம் (எல்லாவற்றிற்கும் மேலாக, இது ஒரு பகுத்தறிவு சமன்பாட்டின் வேர் என்று சொல்ல நாங்கள் பயப்படவில்லை, ஒரு முக்கோணவியல் சமன்பாட்டின் வேர், உண்மையில் இந்த எண்கள் என்ன என்பதைப் பற்றி சிந்திக்காமல்:
எனவே, கணிதவியலாளர்கள் 2^ என்ற குறியீட்டில் என்ன அர்த்தம் வைக்கிறார்கள் என்பதை நாங்கள் கண்டுபிடித்தோம். இதேபோல், a என்றால் என்ன மற்றும் பொதுவாக என்ன என்பதை நீங்கள் தீர்மானிக்கலாம், இதில் a என்பது ஒரு விகிதாசார எண் மற்றும் a > 1.
ஆனால் 0 என்றால் என்ன<а <1? Как вычислить, например, ? Самым естественным способом: считать, что свести вычисления к случаю, когда основание степени больше 1.
இப்போது நாம் தன்னிச்சையான பகுத்தறிவு அடுக்குகளைக் கொண்ட அதிகாரங்களைப் பற்றி மட்டுமல்ல, தன்னிச்சையான உண்மையான அடுக்குகளைக் கொண்ட சக்திகளைப் பற்றியும் பேசலாம். எந்தவொரு உண்மையான அடுக்குகளையும் கொண்ட பட்டங்கள் டிகிரிகளின் அனைத்து வழக்கமான பண்புகளையும் கொண்டிருக்கின்றன என்பது நிரூபிக்கப்பட்டுள்ளது: அதே அடிப்படைகளுடன் சக்திகளைப் பெருக்கும்போது, ​​​​அடுக்குகள் சேர்க்கப்படுகின்றன, வகுக்கும் போது அவை கழிக்கப்படுகின்றன, ஒரு பட்டத்தை ஒரு சக்தியாக உயர்த்தும்போது அவை பெருக்கப்படுகின்றன. ஆனால் மிக முக்கியமான விஷயம் என்னவென்றால், அனைத்து உண்மையான எண்களின் தொகுப்பிலும் வரையறுக்கப்பட்ட y-ax செயல்பாட்டைப் பற்றி இப்போது பேசலாம்.
y = 2 x செயல்பாட்டிற்கு திரும்பி அதன் வரைபடத்தை உருவாக்குவோம். இதைச் செய்ய, y=2x செயல்பாட்டு மதிப்புகளின் அட்டவணையை உருவாக்குவோம்:

ஒருங்கிணைப்பு விமானத்தில் (படம் 194) புள்ளிகளைக் குறிக்கலாம், அவை ஒரு குறிப்பிட்ட கோட்டைக் குறிக்கின்றன, அதை வரைவோம் (படம் 195).

y - 2 x செயல்பாட்டின் பண்புகள்:
1)
2) இரட்டை அல்லது இரட்டை இல்லை; 248
3) அதிகரிக்கிறது;

5) பெரிய அல்லது சிறிய மதிப்புகள் இல்லை;
6) தொடர்ச்சியான;
7)
8) குவிந்த கீழ்நோக்கி.

y-2 x செயல்பாட்டின் பட்டியலிடப்பட்ட பண்புகளின் கடுமையான சான்றுகள் உயர் கணிதத்தின் போக்கில் கொடுக்கப்பட்டுள்ளன. இந்த பண்புகளில் சிலவற்றை ஒரு பட்டம் அல்லது மற்றொன்றுக்கு முன்னர் நாங்கள் விவாதித்தோம், அவற்றில் சில கட்டப்பட்ட வரைபடத்தால் தெளிவாக நிரூபிக்கப்பட்டுள்ளன (படம் 195 ஐப் பார்க்கவும்). எடுத்துக்காட்டாக, ஒரு செயல்பாட்டின் சமநிலை அல்லது ஒற்றைப்படைத்தன்மையின் பற்றாக்குறை, முறையே வரைபடத்தின் சமச்சீர் பற்றாக்குறையுடன் வடிவியல் ரீதியாக தொடர்புடையது, இது y- அச்சுடன் தொடர்புடையது அல்லது தோற்றத்துடன் தொடர்புடையது.

y = a x வடிவத்தின் எந்தச் செயல்பாடும், இங்கு a > 1, ஒத்த பண்புகளைக் கொண்டுள்ளது. படத்தில். ஒரு ஒருங்கிணைப்பு அமைப்பில் 196 கட்டப்பட்டது, y=2 x, y=3 x, y=5 x செயல்பாடுகளின் வரைபடங்கள்.

இப்போது செயல்பாட்டைக் கருத்தில் கொண்டு அதற்கான மதிப்புகளின் அட்டவணையை உருவாக்குவோம்:

ஒருங்கிணைப்பு விமானத்தில் (படம் 197) புள்ளிகளைக் குறிக்கலாம், அவை ஒரு குறிப்பிட்ட கோட்டைக் குறிக்கின்றன, அதை வரைவோம் (படம் 198).

செயல்பாட்டு பண்புகள்

1)
2) இரட்டை அல்லது இரட்டை இல்லை;
3) குறைகிறது;
4) மேலே இருந்து வரம்பற்றது, கீழே இருந்து வரம்புக்குட்பட்டது;
5) பெரிய அல்லது சிறிய மதிப்பு இல்லை;
6) தொடர்ச்சியான;
7)
8) குவிந்த கீழ்நோக்கி.
y = a x வடிவத்தின் எந்தச் செயல்பாடும் ஒத்த பண்புகளைக் கொண்டுள்ளது, அங்கு O<а <1. На рис. 200 в одной системе координат построены графики функций
தயவுசெய்து கவனிக்கவும்: செயல்பாட்டு வரைபடங்கள் அந்த. y=2 x, y அச்சில் சமச்சீர் (படம் 201). இது பொது அறிக்கையின் விளைவாகும் (§ 13 ஐப் பார்க்கவும்): y = f(x) மற்றும் y = f(-x) சார்புகளின் வரைபடங்கள் y-அச்சுக்கு சமச்சீராக இருக்கும். இதேபோல், y = 3 x மற்றும் செயல்பாடுகளின் வரைபடங்கள்

சொல்லப்பட்டதைச் சுருக்கமாக, அதிவேக செயல்பாட்டின் வரையறையை வழங்குவோம் மற்றும் அதன் மிக முக்கியமான பண்புகளை முன்னிலைப்படுத்துவோம்.

வரையறை.படிவத்தின் செயல்பாடு ஒரு அதிவேக செயல்பாடு என்று அழைக்கப்படுகிறது.
அதிவேக செயல்பாட்டின் அடிப்படை பண்புகள் y = a x

a> 1 க்கு y=a x செயல்பாட்டின் வரைபடம் படம். 201, மற்றும் 0க்கு<а < 1 - на рис. 202.

படத்தில் காட்டப்பட்டுள்ள வளைவு. 201 அல்லது 202 ஆனது அடுக்கு எனப்படும். உண்மையில், கணிதவியலாளர்கள் வழக்கமாக அதிவேக செயல்பாட்டையே y = a x என்று அழைக்கிறார்கள். எனவே "அதிவேகம்" என்ற சொல் இரண்டு அர்த்தங்களில் பயன்படுத்தப்படுகிறது: இரண்டும் அதிவேக செயல்பாட்டிற்கு பெயரிட மற்றும் அதிவேக செயல்பாட்டின் வரைபடத்தை பெயரிட. பொதுவாக நாம் ஒரு அதிவேக செயல்பாட்டைப் பற்றி பேசுகிறோமா அல்லது அதன் வரைபடத்தைப் பற்றி பேசுகிறோமா என்பது தெளிவாக இருக்கும்.

y=ax என்ற அதிவேக செயல்பாட்டின் வரைபடத்தின் வடிவியல் அம்சத்திற்கு கவனம் செலுத்துங்கள்: x-அச்சு என்பது வரைபடத்தின் கிடைமட்ட அறிகுறியாகும். உண்மை, இந்த அறிக்கை பொதுவாக பின்வருமாறு தெளிவுபடுத்தப்படுகிறது.
x-அச்சு என்பது செயல்பாட்டின் வரைபடத்தின் கிடைமட்ட அறிகுறியாகும்

வேறு வார்த்தைகளில் கூறுவதானால்

முதல் முக்கியமான குறிப்பு. பள்ளி குழந்தைகள் பெரும்பாலும் விதிமுறைகளை குழப்புகிறார்கள்: சக்தி செயல்பாடு, அதிவேக செயல்பாடு. ஒப்பிடு:

இவை சக்தி செயல்பாடுகளின் எடுத்துக்காட்டுகள்;

இவை அதிவேக செயல்பாடுகளின் எடுத்துக்காட்டுகள்.

பொதுவாக, y = x r, இங்கு r என்பது ஒரு குறிப்பிட்ட எண்ணாக இருக்கும், இது ஒரு சக்தி சார்பு (வாதம் x என்பது பட்டத்தின் அடிப்பகுதியில் உள்ளது);
y = a", இதில் a என்பது ஒரு குறிப்பிட்ட எண்ணாகும் (நேர்மறை மற்றும் 1 இலிருந்து வேறுபட்டது), ஒரு அதிவேகச் சார்பாகும் (வாதம் x என்பது அதிவேகத்தில் உள்ளது).

y = x" போன்ற "அயல்நாட்டு" செயல்பாடு அதிவேகமாகவோ அல்லது சக்தியாகவோ கருதப்படுவதில்லை (இது சில நேரங்களில் அதிவேகமாக அழைக்கப்படுகிறது).

இரண்டாவது முக்கியமான குறிப்பு. பொதுவாக ஒருவர் ஒரு அதிவேக செயல்பாட்டை அடிப்படை a = 1 உடன் அல்லது அடிப்படையுடன் சமத்துவமின்மையை திருப்திப்படுத்துவதாக கருதுவதில்லை.<0 (вы, конечно, помните, что выше, в определении показательной функции, оговорены условия: а >0 மற்றும் a உண்மை என்னவென்றால், a = 1 என்றால், x இன் எந்த மதிப்பிற்கும் Ix = 1 ஆனது, a = 1 உடன் கூடிய y = a" ஒரு நிலையான செயல்பாடாக y = 1 ஆக மாறுகிறது. a = 0 எனில், x இன் எந்த நேர்மறை மதிப்புக்கும் 0x = 0, அதாவது x > 0 க்கு வரையறுக்கப்பட்ட y = 0 செயல்பாட்டைப் பெறுகிறோம் - இறுதியாக, a என்றால் இதுவும் ஆர்வமற்றது.<0, то выражение а" имеет смысл лишь при целых значениях х, а мы все-таки предпочитаем рассматривать функции, определенные на сплошных промежутках.

எடுத்துக்காட்டுகளைத் தீர்ப்பதற்கு முன், அதிவேக செயல்பாடு நீங்கள் இதுவரை படித்த அனைத்து செயல்பாடுகளிலிருந்தும் கணிசமாக வேறுபட்டது என்பதைக் கவனியுங்கள். ஒரு புதிய பொருளை முழுமையாகப் படிக்க, நீங்கள் அதை வெவ்வேறு கோணங்களில், வெவ்வேறு சூழ்நிலைகளில் கருத்தில் கொள்ள வேண்டும், எனவே பல எடுத்துக்காட்டுகள் இருக்கும்.
உதாரணம் 1.

தீர்வு, a) ஒரு ஒருங்கிணைப்பு அமைப்பில் y = 2 x மற்றும் y = 1 செயல்பாடுகளின் வரைபடங்களை உருவாக்கி, அவை ஒரு பொதுவான புள்ளி (0; 1) இருப்பதை நாங்கள் கவனிக்கிறோம் (படம் 203). அதாவது 2x = 1 என்ற சமன்பாடு x =0 என்ற ஒற்றை மூலத்தைக் கொண்டுள்ளது.

எனவே, 2x = 2° சமன்பாட்டிலிருந்து நாம் x = 0 ஐப் பெறுகிறோம்.

b) ஒரு ஒருங்கிணைப்பு அமைப்பில் y = 2 x மற்றும் y = 4 செயல்பாடுகளின் வரைபடங்களை உருவாக்கி, அவை ஒரு பொதுவான புள்ளியைக் கொண்டிருப்பதை (படம் 203) கவனிக்கிறோம் (2; 4). அதாவது 2x = 4 என்ற சமன்பாட்டில் x = 2 என்ற ஒற்றை வேர் உள்ளது.

எனவே, 2 x = 2 2 சமன்பாட்டிலிருந்து நாம் x = 2 ஐப் பெறுகிறோம்.

c) மற்றும் d) அதே பரிசீலனைகளின் அடிப்படையில், சமன்பாடு 2 x = 8 ஒரு ஒற்றை மூலத்தைக் கொண்டுள்ளது என்று முடிவு செய்கிறோம், அதைக் கண்டுபிடிக்க, தொடர்புடைய செயல்பாடுகளின் வரைபடங்கள் உருவாக்கப்பட வேண்டியதில்லை;

2 3 = 8 என்பதால் x = 3 என்பது தெளிவாகிறது. இதேபோல், சமன்பாட்டின் ஒரே மூலத்தைக் காண்கிறோம்

எனவே, 2x = 2 3 சமன்பாட்டிலிருந்து நாம் x = 3 ஐப் பெற்றோம், மேலும் 2 x = 2 x சமன்பாட்டிலிருந்து x = -4 ஐப் பெற்றோம்.
இ) y = 2 x செயல்பாட்டின் வரைபடம் x >0 க்கு y = 1 செயல்பாட்டின் வரைபடத்திற்கு மேலே அமைந்துள்ளது - இது படத்தில் தெளிவாகப் படிக்கக்கூடியது. 203. சமத்துவமின்மைக்கான தீர்வு 2x > 1 என்பது இடைவெளி
e) y = 2 x செயல்பாட்டின் வரைபடம் y = 4 செயல்பாட்டின் வரைபடத்திற்கு கீழே x இல் அமைந்துள்ளது<2 - это хорошо читается по рис. 203. Значит, решением неравенства 2х <4служит промежуток
உதாரணம் 1 ஐ தீர்க்கும் போது எடுக்கப்பட்ட அனைத்து முடிவுகளுக்கும் அடிப்படையானது y = 2 x செயல்பாட்டின் மோனோடோனிசிட்டி (அதிகரிப்பு) பண்பு என்பதை நீங்கள் கவனித்திருக்கலாம். இதே போன்ற பகுத்தறிவு பின்வரும் இரண்டு கோட்பாடுகளின் செல்லுபடியை சரிபார்க்க அனுமதிக்கிறது.

தீர்வு.நீங்கள் இவ்வாறு தொடரலாம்: y-3 x செயல்பாட்டின் வரைபடத்தை உருவாக்கவும், பின்னர் அதை x அச்சில் இருந்து 3 காரணி மூலம் நீட்டி, அதன் விளைவாக வரைபடத்தை 2 அளவு அலகுகளால் உயர்த்தவும். ஆனால் 3- 3* =3 *+1 என்ற உண்மையைப் பயன்படுத்துவது மிகவும் வசதியானது, எனவே, y=3 x*1 + 2 செயல்பாட்டின் வரைபடத்தை உருவாக்கவும்.

இதுபோன்ற சந்தர்ப்பங்களில் நாம் பல முறை செய்ததைப் போல, புள்ளியில் (-1; 2) - புள்ளியிடப்பட்ட கோடுகள் x = - 1 மற்றும் 1x = 2 இல் உள்ள ஒரு துணை ஒருங்கிணைப்பு அமைப்புக்கு செல்லலாம். 207. புதிய ஒருங்கிணைப்பு அமைப்பில் y=3* செயல்பாட்டை "இணைப்போம்". இதைச் செய்ய, செயல்பாட்டிற்கான கட்டுப்பாட்டு புள்ளிகளைத் தேர்ந்தெடுக்கவும் , ஆனால் அவற்றை பழையவற்றில் அல்ல, புதிய ஒருங்கிணைப்பு அமைப்பில் உருவாக்குவோம் (இந்த புள்ளிகள் படம் 207 இல் குறிக்கப்பட்டுள்ளன). பின்னர் புள்ளிகளில் இருந்து ஒரு அடுக்கு உருவாக்குவோம் - இது தேவையான வரைபடமாக இருக்கும் (படம் 207 ஐப் பார்க்கவும்).
[-2, 2] பிரிவில் கொடுக்கப்பட்ட செயல்பாட்டின் மிகப்பெரிய மற்றும் சிறிய மதிப்புகளைக் கண்டறிய, கொடுக்கப்பட்ட செயல்பாடு அதிகரித்து வருகிறது என்ற உண்மையைப் பயன்படுத்திக் கொள்கிறோம், எனவே அது முறையே அதன் சிறிய மற்றும் பெரிய மதிப்புகளை எடுத்துக்கொள்கிறது. பிரிவின் இடது மற்றும் வலது முனைகள்.
எனவே:

எடுத்துக்காட்டு 4.சமன்பாடு மற்றும் ஏற்றத்தாழ்வுகளை தீர்க்கவும்:

தீர்வு, a) ஒரு ஒருங்கிணைப்பு அமைப்பில் y=5* மற்றும் y=6-x செயல்பாடுகளின் வரைபடங்களை உருவாக்குவோம் (படம் 208). அவை ஒரு புள்ளியில் வெட்டுகின்றன; வரைபடத்தின் மூலம் மதிப்பிடுவது, இது புள்ளி (1; 5). உண்மையில் புள்ளி (1; 5) சமன்பாடு y = 5* மற்றும் சமன்பாடு y = 6-x இரண்டையும் திருப்திப்படுத்துகிறது என்பதை சரிபார்ப்பு காட்டுகிறது. இந்த புள்ளியின் abscissa கொடுக்கப்பட்ட சமன்பாட்டின் ஒரே வேராக செயல்படுகிறது.

எனவே, 5 x = 6 - x என்ற சமன்பாடு x = 1 என்ற ஒற்றை மூலத்தைக் கொண்டுள்ளது.

b) மற்றும் c) y-5x என்ற அடுக்கு y=6-x என்ற நேர் கோட்டிற்கு மேலே உள்ளது, x>1 எனில், இது படத்தில் தெளிவாகத் தெரியும். 208. அதாவது சமத்துவமின்மை 5*>6க்கான தீர்வை பின்வருமாறு எழுதலாம்: x>1. மற்றும் சமத்துவமின்மைக்கான தீர்வு 5x<6 - х можно записать так: х < 1.
பதில்: a)x = 1; b)x>1; c)x<1.

எடுத்துக்காட்டு 5.ஒரு செயல்பாடு வழங்கப்பட்டது என்பதை நிரூபியுங்கள்
தீர்வு.நாம் வைத்திருக்கும் நிபந்தனையின்படி.

அதிவேக மற்றும் மடக்கை செயல்பாடுகள் VIII

§ 179 அதிவேக செயல்பாட்டின் அடிப்படை பண்புகள்

இந்த பகுதியில் நாம் அதிவேக செயல்பாட்டின் அடிப்படை பண்புகளை படிப்போம்

y = a x (1)

அதை கீழே நினைவில் கொள்வோம் ஏ சூத்திரத்தில் (1) 1 ஐத் தவிர வேறு ஏதேனும் நிலையான நேர்மறை எண்ணைக் குறிக்கிறோம்.

சொத்து 1. ஒரு அதிவேக செயல்பாட்டின் டொமைன் அனைத்து உண்மையான எண்களின் தொகுப்பாகும்.

உண்மையில், நேர்மறையுடன் ஏ வெளிப்பாடு ஏ x எந்த உண்மையான எண்ணுக்கும் வரையறுக்கப்பட்டுள்ளது எக்ஸ் .

சொத்து 2. அதிவேக செயல்பாடு நேர்மறை மதிப்புகளை மட்டுமே ஏற்றுக்கொள்கிறது.

உண்மையில், என்றால் எக்ஸ் > 0, பின்னர், § 176 இல் நிரூபிக்கப்பட்டது,

ஏ x > 0.

என்றால் எக்ஸ் <. 0, то

ஏ x =

எங்கே - எக்ஸ் ஏற்கனவே பூஜ்ஜியத்தை விட அதிகமாக உள்ளது. அதனால் தான் A - x > 0. ஆனால் பின்னர்

ஏ x = > 0.

இறுதியாக, எப்போது எக்ஸ் = 0

ஏ x = 1.

அதிவேக செயல்பாட்டின் 2 வது பண்பு ஒரு எளிய வரைகலை விளக்கத்தைக் கொண்டுள்ளது. இந்த செயல்பாட்டின் வரைபடம் (படம் 246 மற்றும் 247 ஐப் பார்க்கவும்) முற்றிலும் abscissa அச்சுக்கு மேலே அமைந்துள்ளது.

சொத்து 3. என்றால் ஏ >1, பிறகு எப்போது எக்ஸ் > 0 ஏ x > 1, மற்றும் எப்போது எக்ஸ் < 0 ஏ x < 1. என்றால் ஏ < 1, тஓ, மாறாக, எப்போது எக்ஸ் > 0 ஏ x < 1, மற்றும் எப்போது எக்ஸ் < 0 ஏ x > 1.

அதிவேக செயல்பாட்டின் இந்த பண்பு ஒரு எளிய வடிவியல் விளக்கத்தையும் அனுமதிக்கிறது. மணிக்கு ஏ > 1 (படம் 246) வளைவுகள் y = a x நேர் கோட்டிற்கு மேலே அமைந்துள்ளது மணிக்கு = 1 மணிக்கு எக்ஸ் > 0 மற்றும் நேர் கோட்டிற்கு கீழே மணிக்கு = 1 மணிக்கு எக்ஸ் < 0.

என்றால் ஏ < 1 (рис. 247), то, наоборот, кривые y = a x நேர் கோட்டிற்கு கீழே அமைந்துள்ளது மணிக்கு = 1 மணிக்கு எக்ஸ் > 0 மற்றும் இந்த வரிக்கு மேல் எக்ஸ் < 0.

3வது சொத்துக்கு கடுமையான ஆதாரம் தருவோம். விடுங்கள் ஏ > 1 மற்றும் எக்ஸ் - ஒரு தன்னிச்சையான நேர்மறை எண். அதைக் காட்டுவோம்

ஏ x > 1.

எண் என்றால் எக்ஸ் பகுத்தறிவு ( எக்ஸ் = மீ / n ), அது ஏ x = ஏ மீ/ n = n √அ மீ .

இருந்து ஏ > 1, பின்னர் ஏ மீ > 1, ஆனால் ஒன்றை விட பெரிய எண்ணின் மூலமும் 1 ஐ விட அதிகமாக உள்ளது.

என்றால் எக்ஸ் பகுத்தறிவற்றது, பின்னர் நேர்மறை பகுத்தறிவு எண்கள் உள்ளன X" மற்றும் X" , இது ஒரு எண்ணின் தசம தோராயமாக செயல்படுகிறது x :

X"< х < х" .

ஆனால் பின்னர், ஒரு பகுத்தறிவற்ற அடுக்குடன் ஒரு பட்டத்தின் வரையறை

ஏ x" < ஏ x < ஏ x"" .

மேலே காட்டப்பட்டுள்ளபடி, எண் ஏ x" ஒன்றுக்கு மேற்பட்டவை. எனவே எண் ஏ x , விட பெரியது ஏ x" , 1 ஐ விட அதிகமாக இருக்க வேண்டும்,

எனவே, எப்போது என்பதை நாங்கள் காட்டியுள்ளோம் அ >1 மற்றும் தன்னிச்சையான நேர்மறை எக்ஸ்

ஏ x > 1.

எண் என்றால் எக்ஸ் எதிர்மறையாக இருந்தது, அப்போது நாம் பெற்றிருப்போம்

ஏ x =

எண் எங்கே எக்ஸ் ஏற்கனவே நேர்மறையாக இருக்கும். அதனால் தான் A - x > 1. எனவே,

ஏ x = < 1.

எனவே, எப்போது ஏ > 1 மற்றும் தன்னிச்சையான எதிர்மறை x

ஏ x < 1.

வழக்கு 0< ஏ < 1, легко сводится к уже рассмотренному случаю. Учащимся предлагается убедиться в этом самостоятельно.

சொத்து 4. x என்றால் = 0, பின்னர் பொருட்படுத்தாமல் ஒரு ஏ x =1.

இது டிகிரி பூஜ்ஜியத்தின் வரையறையிலிருந்து பின்வருமாறு; பூஜ்ஜியத்தைத் தவிர வேறு எந்த எண்ணின் பூஜ்ஜிய சக்தியும் 1 க்கு சமம். வரைபட ரீதியாக, இந்தப் பண்பு எதற்கும் ஏ வளைவு மணிக்கு = ஏ x (படம் 246 மற்றும் 247 ஐப் பார்க்கவும்) அச்சை வெட்டுகிறது மணிக்கு ஆர்டினேட் 1 உடன் ஒரு கட்டத்தில்.

சொத்து 5. மணிக்கு ஏ >1 அதிவேக செயல்பாடு = ஏ x ஏகபோகமாக அதிகரித்து வருகிறது, மற்றும் ஒரு < 1 - ஏகபோகமாக குறைகிறது.

இந்த சொத்து ஒரு எளிய வடிவியல் விளக்கத்தையும் அனுமதிக்கிறது.

மணிக்கு ஏ > 1 (படம் 246) வளைவு மணிக்கு = ஏ x வளர்ச்சியுடன் எக்ஸ் மேலும் உயரும், எப்போது ஏ < 1 (рис. 247) - опускается все ниже и ниже.

5வது சொத்தின் கடுமையான ஆதாரத்தை தருவோம்.

விடுங்கள் ஏ > 1 மற்றும் எக்ஸ் 2 > எக்ஸ் 1. அதைக் காட்டுவோம்

ஏ x 2 > ஏ x 1

இருந்து எக்ஸ் 2 > எக்ஸ் 1., பின்னர் எக்ஸ் 2 = எக்ஸ் 1 + ஈ , எங்கே ஈ - சில நேர்மறை எண். அதனால் தான்

ஏ x 2 - ஏ x 1 = ஏ x 1 + ஈ - ஏ x 1 = ஏ x 1 (ஏ ஈ - 1)

அதிவேக செயல்பாட்டின் 2 வது பண்பு மூலம் ஏ x 1 > 0. முதல் ஈ > 0, பின்னர் அதிவேக செயல்பாட்டின் 3வது பண்பு மூலம் ஏ ஈ > 1. தயாரிப்பு இரண்டு காரணிகள் ஏ x 1 (ஏ ஈ - 1) நேர்மறை, எனவே இந்த தயாரிப்பு நேர்மறையானது. பொருள் ஏ x 2 - ஏ x 1 > 0, அல்லது ஏ x 2 > ஏ x 1, இது நிரூபிக்கப்பட வேண்டும்.

எனவே, எப்போது அ > 1 செயல்பாடு மணிக்கு = ஏ x ஏகமாக அதிகரித்து வருகிறது. இதேபோல், எப்போது என்பது நிரூபிக்கப்பட்டுள்ளது ஏ < 1 функция மணிக்கு = ஏ x ஏகபோகமாக குறைந்து வருகிறது.

விளைவு. 1 ஐத் தவிர ஒரே நேர்மறை எண்ணின் இரண்டு சக்திகள் சமமாக இருந்தால், அவற்றின் அடுக்குகள் சமமாக இருக்கும்.

வேறு வார்த்தைகளில் கூறுவதானால், என்றால்

ஏ பி = ஏ c (ஏ > 0 மற்றும் ஏ =/= 1),

b = c .

உண்மையில், எண்கள் என்றால் பி மற்றும் உடன் சமமாக இல்லை, பின்னர் செயல்பாட்டின் மோனோடோனிசிட்டி காரணமாக மணிக்கு = ஏ x அவற்றில் பெரியது ஒத்திருக்கும் ஏ >1 பெரியது, எப்போது ஏ < 1 меньшее значение этой функции. Таким образом, было бы или ஏ பி > ஏ c , அல்லது ஏ பி < ஏ c . இரண்டும் நிபந்தனைக்கு முரணானவை ஏ பி = ஏ c . அதை ஒப்புக்கொள்ள வேண்டியதுதான் b = c .

சொத்து 6. ஒரு என்றால் > 1, பின்னர் வாதத்தில் வரம்பற்ற அதிகரிப்புடன் எக்ஸ் (எக்ஸ் -> ∞ ) செயல்பாட்டு மதிப்புகள் மணிக்கு = ஏ x காலவரையின்றி வளரும் (மணிக்கு -> ∞ ). வாதம் வரம்பில்லாமல் குறையும் போது எக்ஸ் (எக்ஸ் -> -∞ ) நேர்மறையாக இருக்கும் போது இந்த செயல்பாட்டின் மதிப்புகள் பூஜ்ஜியமாக இருக்கும் (மணிக்கு->0; மணிக்கு > 0).

மேலே நிரூபிக்கப்பட்ட செயல்பாட்டின் மோனோடோனிசிட்டியை கணக்கில் எடுத்துக்கொள்வது மணிக்கு = ஏ x , பரிசீலனையில் உள்ள வழக்கில் செயல்பாடு என்று நாம் கூறலாம் மணிக்கு = ஏ x ஏகபோகமாக 0 முதல் அதிகரிக்கிறது ∞ .

என்றால் 0 <ஏ < 1, x (x -> ∞) வாதத்தில் வரம்பற்ற அதிகரிப்புடன், y = a x செயல்பாட்டின் மதிப்புகள் பூஜ்ஜியமாக இருக்கும், அதே சமயம் நேர்மறையாக இருக்கும் (மணிக்கு->0; மணிக்கு > 0). வாதம் x வரம்பில்லாமல் குறையும் போது (எக்ஸ் -> -∞ ) இந்த செயல்பாட்டின் மதிப்புகள் வரம்பற்ற அளவில் வளரும் (மணிக்கு -> ∞ ).

செயல்பாட்டின் மோனோடோனிசிட்டி காரணமாக y = a x இந்த விஷயத்தில் செயல்பாடு என்று நாம் கூறலாம் மணிக்கு = ஏ x இருந்து ஏகபோகமாக குறைகிறது ∞ 0 வரை.

அதிவேக செயல்பாட்டின் 6 வது பண்பு, புள்ளிவிவரங்கள் 246 மற்றும் 247 இல் தெளிவாக பிரதிபலிக்கிறது. நாங்கள் அதை கண்டிப்பாக நிரூபிக்க மாட்டோம்.

நாம் செய்ய வேண்டியது அதிவேக செயல்பாட்டின் மாறுபாட்டின் வரம்பை நிறுவுவதுதான் y = a x (ஏ > 0, ஏ =/= 1).

செயல்பாடு என்பதை மேலே நிரூபித்தோம் y = a x நேர்மறை மதிப்புகளை மட்டுமே எடுத்துக்கொள்கிறது மற்றும் 0 முதல் ஏகபோகமாக அதிகரிக்கிறது ∞ (அதில் ஏ > 1), அல்லது ஏகபோகமாக குறைகிறது ∞ 0 க்கு (0 மணிக்கு< ஏ <. 1). Однако остался невыясненным следующий вопрос: не претерпевает ли функция y = a x நீங்கள் மாறும்போது ஏதேனும் தாவல்கள் உள்ளதா? இது ஏதேனும் நேர்மறையான மதிப்புகளை எடுக்குமா? இந்த பிரச்சினை நேர்மறையாக தீர்க்கப்படுகிறது. என்றால் ஏ > 0 மற்றும் ஏ =/= 1, நேர்மறை எண் எதுவாக இருந்தாலும் சரி மணிக்கு 0 கண்டிப்பாக காணப்படும் எக்ஸ் 0, அது போன்றது

ஏ x 0 = மணிக்கு 0 .

(செயல்பாட்டின் மோனோடோனிசிட்டி காரணமாக y = a x குறிப்பிட்ட மதிப்பு எக்ஸ் 0, நிச்சயமாக, ஒரே ஒன்றாக இருக்கும்.)

இந்த உண்மையை நிரூபிப்பது எங்கள் திட்டத்தின் எல்லைக்கு அப்பாற்பட்டது. அதன் வடிவியல் விளக்கம் என்பது எதற்கும் நேர்மறை மதிப்பு மணிக்கு 0 செயல்பாடு வரைபடம் y = a x கண்டிப்பாக நேர்கோட்டுடன் வெட்டும் மணிக்கு = மணிக்கு 0 மற்றும், மேலும், ஒரு கட்டத்தில் மட்டுமே (படம் 248).

இதிலிருந்து நாம் பின்வரும் முடிவை எடுக்கலாம், அதை நாம் சொத்து 7 என உருவாக்குகிறோம்.

சொத்து 7. அதிவேக செயல்பாட்டின் மாற்றத்தின் பகுதி y = a x (ஏ > 0, ஏ =/= 1)அனைத்து நேர்மறை எண்களின் தொகுப்பாகும்.

பயிற்சிகள்

1368. பின்வரும் செயல்பாடுகளின் வரையறையின் களங்களைக் கண்டறியவும்:

1369. இந்த எண்களில் எது 1 ஐ விட பெரியது மற்றும் 1 ஐ விட குறைவானது:

1370. அதிவேக செயல்பாட்டின் எந்தப் பண்புகளின் அடிப்படையில் அதைக் குறிப்பிடலாம்

a) (5 / 7) 2.6 > (5 / 7) 2.5; b) (4 / 3) 1.3 > (4 / 3) 1.2

1371. எந்த எண் பெரியது:

A) π - √3 அல்லது (1/ π ) - √3 ; c) (2/3) 1 + √6 அல்லது (2/3) √2 + √5 ;

b) ( π / 4) 1 + √3 அல்லது ( π / 4) 2; ஈ) (√3) √2 - √5 அல்லது (√3) √3 - 2 ?

1372. சமத்துவமின்மைகள் சமமானவையா:

1373. எண்களைப் பற்றி என்ன சொல்ல முடியும் எக்ஸ் மற்றும் மணிக்கு , என்றால் ஒரு x = மற்றும் ஒய் , எங்கே ஏ - கொடுக்கப்பட்ட நேர்மறை எண்?

1374. 1) செயல்பாட்டின் அனைத்து மதிப்புகளிலும் இது சாத்தியமா மணிக்கு = 2x முன்னிலைப்படுத்த:

2) செயல்பாட்டின் அனைத்து மதிப்புகளிலும் இது சாத்தியமா? மணிக்கு = 2 | x| முன்னிலைப்படுத்த:

A) மிக உயர்ந்த மதிப்பு; b) சிறிய மதிப்பு?

முதலில் ஒரு அதிவேக செயல்பாட்டின் வரையறையை அறிமுகப்படுத்துவோம்.

அதிவேக செயல்பாடு $f\left(x\right)=a^x$, இங்கு $a >1$.

$a >1$க்கான அதிவேக செயல்பாட்டின் பண்புகளை அறிமுகப்படுத்துவோம்.

\\[வேர்கள் இல்லை\] \

ஒருங்கிணைப்பு அச்சுகளுடன் வெட்டும். செயல்பாடு $Ox$ அச்சில் குறுக்கிடவில்லை, ஆனால் $(0,1)$ புள்ளியில் $Oy$ அச்சை வெட்டுகிறது.

$f""\left(x\right)=(\left(a^xlna\right))"=a^x(ln)^2a$

\\[வேர்கள் இல்லை\] \

வரைபடம் (படம் 1).

படம் 1. செயல்பாட்டின் வரைபடம் $f\left(x\right)=a^x,\ for\ a >1$.

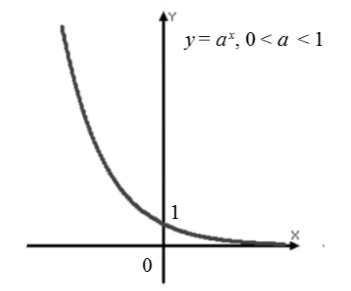
அதிவேக செயல்பாடு $f\left(x\right)=a^x$, இங்கு $0

அதிவேக செயல்பாட்டின் பண்புகளை $0 இல் அறிமுகப்படுத்துவோம்

வரையறையின் களம் அனைத்தும் உண்மையான எண்கள்.

$f\left(-x\right)=a^(-x)=\frac(1)(a^x)$ -- செயல்பாடு சமமாகவோ அல்லது ஒற்றைப்படையாகவோ இல்லை.

$f(x)$ என்பது வரையறையின் முழுக் களத்திலும் தொடர்கிறது.

மதிப்புகளின் வரம்பு இடைவெளி $(0,+\infty)$ ஆகும்.

$f"(x)=\left(a^x\right)"=a^xlna$

\ \[வேர்கள் இல்லை\] \ \[வேர்கள் இல்லை\] \

செயல்பாடு வரையறையின் முழு களத்திலும் குவிந்துள்ளது.

டொமைனின் முனைகளில் நடத்தை:

\[(\mathop(lim)_(x\to -\infty ) a^x\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) a^x\ ) =0\]

வரைபடம் (படம் 2).

அதிவேக செயல்பாட்டை உருவாக்குவதற்கான சிக்கலின் எடுத்துக்காட்டு

$y=2^x+3$ செயல்பாட்டை ஆராய்ந்து திட்டமிடவும்.

தீர்வு.

மேலே உள்ள எடுத்துக்காட்டு வரைபடத்தைப் பயன்படுத்தி ஒரு ஆய்வை மேற்கொள்வோம்:

வரையறையின் களம் அனைத்தும் உண்மையான எண்கள்.

$f\left(-x\right)=2^(-x)+3$ -- செயல்பாடு சமமாகவோ அல்லது ஒற்றைப்படையாகவோ இல்லை.

$f(x)$ என்பது வரையறையின் முழுக் களத்திலும் தொடர்கிறது.

மதிப்புகளின் வரம்பு இடைவெளி $(3,+\infty)$ ஆகும்.

$f"\left(x\right)=(\left(2^x+3\right))"=2^xln2>0$

வரையறையின் முழு களத்திலும் செயல்பாடு அதிகரிக்கிறது.

வரையறையின் முழு டொமைன் முழுவதும் $f(x)\ge 0$.

ஒருங்கிணைப்பு அச்சுகளுடன் வெட்டும். செயல்பாடு $Ox$ அச்சில் குறுக்கிடவில்லை, ஆனால் $Oy$ அச்சை ($0,4)$ புள்ளியில் வெட்டுகிறது

$f""\left(x\right)=(\left(2^xln2\right))"=2^x(ln)^22>0$

செயல்பாடு வரையறையின் முழு களத்திலும் குவிந்துள்ளது.

டொமைனின் முனைகளில் நடத்தை:

\[(\mathop(lim)_(x\to -\infty ) a^x\ )=0\] \[(\mathop(lim)_(x\to +\infty ) a^x\ )=+ \infty\]

வரைபடம் (படம் 3).

படம் 3. செயல்பாட்டின் வரைபடம் $f\left(x\right)=2^x+3$